LOIS CLASSIQUES DE VARIATION DES VITESSES

Mise en situation

On souhaite déplacer une charge horizontalement sur une certaine distance et en un temps donné. On se demande si la loi de variation des vitesses a une influence sur la puissance que doit avoir le moteur et sur sa consommation. On se propose d'étudier et de comparer plusieurs solutions.

Hypothèses et données

Sur la représentation graphique ci-dessous, la distance parcourue X et le temps total T du cycle sont les mêmes quelle que soit la courbe choisie.

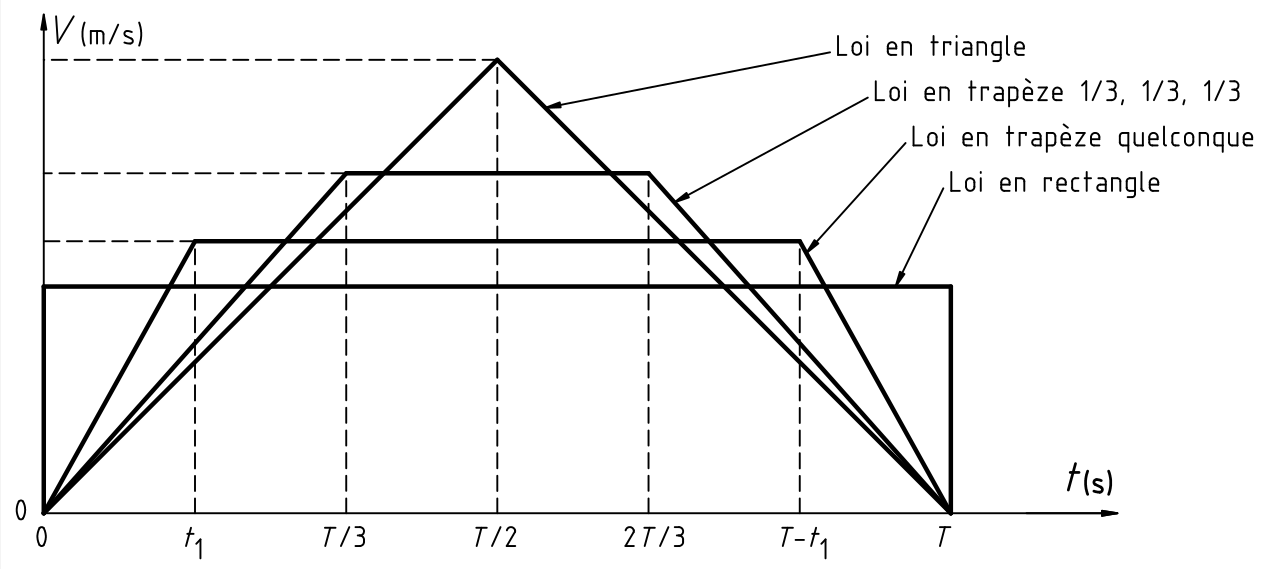
Les frottements étant négligés, la puissance du moteur nécessaire pour déplacer une masse m horizontalement se calcule avec l'expression :

P = m . ∂ . V

m : Masse de la charge, en kg.
∂ : Accélération de la charge, en m/s².
V : Vitesse de la charge, en m/s.
P : Puissance nécessaire pour déplacer la charge, en W.

Etude demandée

1. Déterminer, dans chaque cas et sous forme littérale, la vitesse maximale V_max atteinte, en fonction de X et T.
2. En déduire, en fonction de X et T, l'accélération au démarrage dans chacun des cas.
3. Déterminer l'expression de la puissance nécessaire, dans le cas de la loi trapézoïdale 1/3, 1/3, 1/3.
4. Idem dans le cas de la loi en triangle.
5. Application numérique : X = 11 m, T = 6 s et m = 480 kg.
6. Calculer l'énergie consommée par le moteur au démarrage, dans le cas de la loi trapézoïdale 1/3, 1/3, 1/3.
7. Idem dans le cas de la loi en triangle.
8. Comparer les deux cas, du point de vue de la puissance mécanique et de l'énergie consommée.