LIAISONS EN PARALLELE

Mise en situation

Deux pièces sont reliées entre elles par deux liaisons en parallèle. On cherche à déterminer les caractéristiques de la liaison équivalente.

Hypothèses et données

• Les pièces sont repérées 1 et 2.
• Elles sont reliés entre elles par deux liaisons (L₁) et (L₂) en parallèle.
• Les liaisons (L₁) et (L₂) sont considérées parfaites.
• La pièce 1 exerce sur la pièce 2 deux actions mécaniques aux niveaux des liaisons (L₁) et (L₂). On note respectivement {T₁} et {T₂} les torseurs des actions mécaniques transmissibles par ces liaisons.

Etude demandée

Pour chacun des cas ci-dessous :

1. Ecrire les torseurs {T₁} et {T₂} aux points de liaison sous les formes vectorielle et analytique.
2. Ecrire le torseur {T₂} au point de calcul A.
3. En déduire le torseur d'action mécanique de la liaison équivalente {T_éq.} = {T₁} + {T₂}.
4. A quoi les liaisons (L₁) et (L₂) sont-elles équivalentes?
5. Indiquer le nombre total N_s d'inconnues dans les torseurs {T₁} et {T₂}.
6. Quel nombre r_s d'équations indépendantes (nombre de composantes du torseur {T_éq.} non nulles) est-il possible d'écrire?
7. En déduire le degré de mobilité m = 6 - r_s de la liaison équivalente.
8. Déterminer le degré d'hyperstatisme h = N_s - r_s de la liaison équivalente.

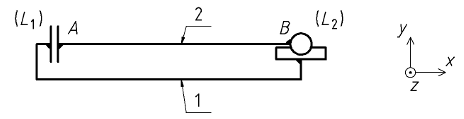
Cas 1 :

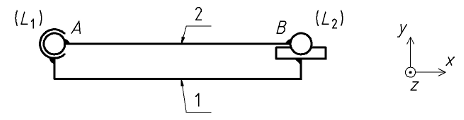
Cas 2 :

Cas 3 :

Cas 4 :