MOMENTS QUADRATIQUES

Mise en situation

Lors d'une étude de rdm, on recherche quelques caractéristiques de poutres de sections connues.

Hypothèses et données

• Différentes sections droites de poutres sont définies ci-dessous :

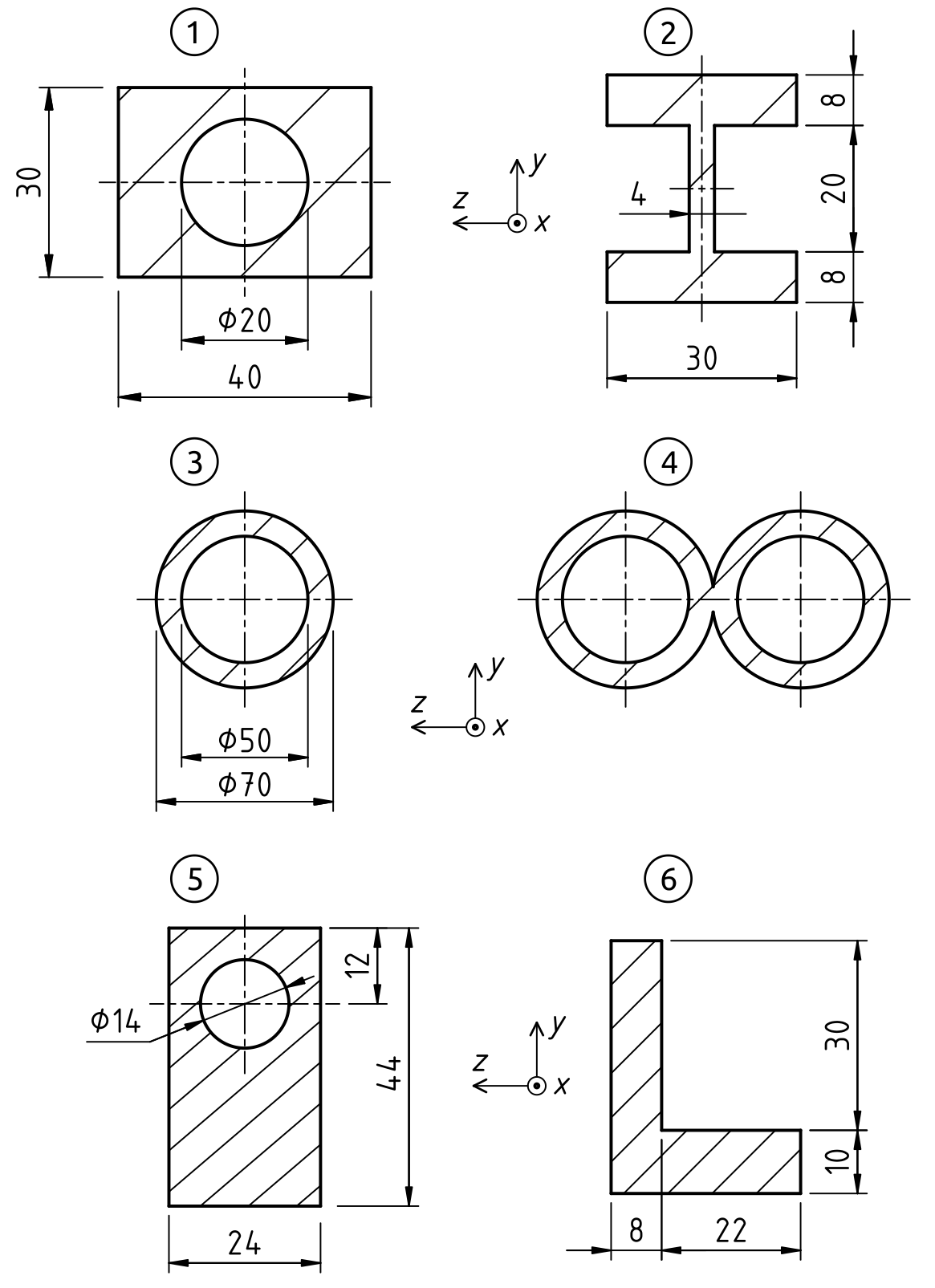
• Les matériaux constituant les poutres sont homogènes et isotropes.

Etude demandée

Pour chacune des sections droites :

1. Calculer la superficie S, en mm².
2. Positionner le barycentre G de la section.
3. Déterminer les moments quadratiques I_Gx, I_Gy et I_Gz, en mm⁴.