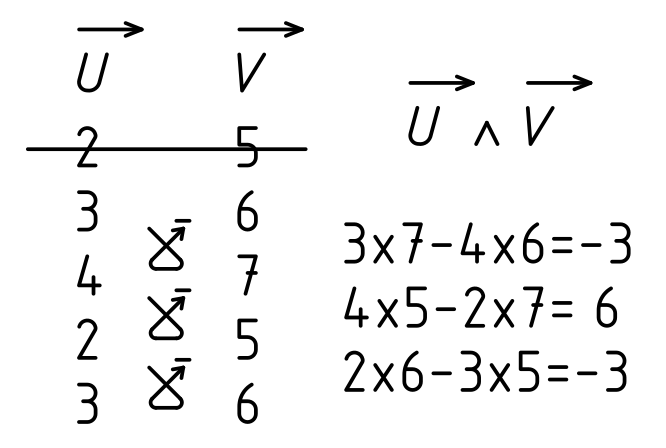LES VECTEURS

Introduction

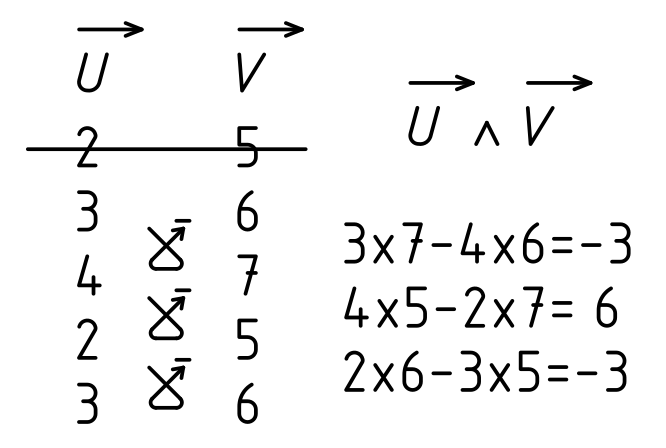
Si on indique, par exemple, une vitesse du vent de 20 km/h, on ne sait pas si le vent vient du nord, de l'ouest ou du sud-est. Pour cette raison, il est commode de définir la vitesse avec un vecteur. Il permet de connaître, en plus de la force du vent, sa direction et son sens.

La mécanique s'appuie sur les mathématiques. Si certaines grandeurs se définissent avec un nombre généralement suivi d'une unité, d'autres grandeurs s'expriment avantageusement avec des vecteurs.

Notion de vecteur

Définition

Le vecteur est un outil mathématique qui définit :

• Une direction.
• Un sens.
• Une norme (ou intensité).

Remarques :

• Pour une direction donnée, il y a deux sens possibles.
• En mécanique, on travaille usuellement :
  • Dans un repère orthonormé direct noté ( O; [vec]x[/vec], [vec]y[/vec], [vec]z[/vec] )
  • En coordonnées cartésiennes.
• Les coordonnées d'un vecteur s'écrivent dans la base orthonormée directe, notée ( [vec]x[/vec], [vec]y[/vec], [vec]z[/vec] ).

Soit [vec]V [/vec] un vecteur de coordonnées a, b et c. Les notations ci-dessous sont équivalentes :

• [vec]V [/vec]  ( a ; b ; c )
• [vec]V [/vec] [barG]a
  b
  c[/barG]
• [vec]V [/vec] = a . [vec]x[/vec] + b . [vec]y[/vec] + c . [vec]z[/vec]

Coordonnées d'un vecteur défini par deux points

Soient A et B deux points de coordonnées connues : A ( x_A ; y_A ; z_A ) et B ( x_B ; y_B ; z_B )

On a : [vec]AB [/vec] ( x_B-x_A ; y_B-y_A ; z_B-z_A )

Norme d'un vecteur

Soit [vec]V [/vec] un vecteur de coordonnées a, b et c connues. La norme de [vec]V [/vec] se calcule avec la relation :

[mod] [vec]V [/vec] [/mod] = [rac]a² + b² + c²[/rac]

Angle orienté d'un couple de vecteurs

L'angle orienté entre deux vecteurs [vec]U [/vec] et [vec]V [/vec] se note ( [ang][vec]U[/vec] ; [vec]V [/vec][/ang] ).

Pour un même angle orienté, il existe une infinité de mesures. La mesure principale appartient à l'intervalle ] – π ; π ]. Une mesure peut être positive ou négative, le sens trigonométrique étant positif et le sens horaire négatif.

Pour une mesure α connue on écrit :

• De manière rigoureuse : α + k.2.π = ( [ang][vec]U[/vec] ; [vec]V [/vec][/ang] )     avec k ∈ ℤ
• Ou plus simplement :   α = ( [ang][vec]U[/vec] ; [vec]V [/vec][/ang] )

Coordonnées d'un vecteur dans le plan

Soit le vecteur [vec]V [/vec] parallèle au plan (Oxy) dont l'angle orienté α = ( [ang][vec]x[/vec] ; [vec]V [/vec][/ang] ) et la norme sont connus.

Les coordonnées a, b et 0 de [vec]V [/vec] se calculent avec les relations :

a = [mod][vec]V [/vec][/mod].cos(α)

b = [mod][vec]V [/vec][/mod].sin(α)

En somme :  [vec]V [/vec] [par][mod][vec]V [/vec][/mod].cos(α) ; [mod][vec]V [/vec][/mod].sin(α) ; 0[/par]

Direction d'un vecteur dans le plan

Soit le vecteur [vec]V [/vec] parallèle au plan (Oxy), dont les coordonnées a b et 0 sont connues.

Les angles orientés α = ([ang]a.[vec]x[/vec], [vec]V [/vec][/ang]) et β = ([ang][vec]V [/vec], b.[vec]y[/vec][/ang]) se calculent avec les relations :

tan(α) = [div]b[sur]a[/div]    ⇒    α = Arctan[par][div]b[sur]a[/div][/par]

tan(β) = [div]a[sur]b[/div]    ⇒    β = Arctan[par][div]a[sur]b[/div][/par]

β = 90° - α

Produit scalaire

Définition

Soit deux vecteurs [vec]U[/vec] et [vec]V[/vec] et α = ( [ang][vec]U[/vec] ; [vec]V [/vec][/ang] ). Le produit scalaire de [vec]U[/vec] par [vec]V[/vec], noté [vec]U[/vec] . [vec]V[/vec], est le nombre réel tel que :

[vec]U[/vec] . [vec]V[/vec] = [mod][vec]U[/vec][/mod] × [mod][vec]V[/vec][/mod] × cos α

Propriétés

• [vec]U[/vec] . [vec]V [/vec] = 0    si    [vec]U[/vec] ⊥ [vec]V[/vec]    ou    [vec]U[/vec] = [vec]0[/vec]    ou    [vec]V [/vec] = [vec]0[/vec].
• [vec]U[/vec] . [vec]V[/vec] = [vec]V[/vec] . [vec]U[/vec]
• [vec]U[/vec] . [vec]V[/vec] = [mod][vec]U[/vec][/mod] × [mod][vec]V[/vec][/mod]    si    α = 0°
• [vec]U[/vec] . [vec]V[/vec] = - [mod][vec]U[/vec][/mod] ×[mod][vec]V [/vec][/mod]    si    α = 180°

Expression analytique

Si    [vec]U[/vec] (u₁; u₂; u₃)    et    [vec]V [/vec] (v₁; v₂; v₃)    alors    [vec]U[/vec] . [vec]V[/vec] = u₁.v₁+u₂.v₂+u₃.v₃

Produit vectoriel

Définition

Soit deux vecteurs [vec]U[/vec] et [vec]V[/vec] et α = ( [ang][vec]U[/vec] ; [vec]V [/vec][/ang] ). Le produit vectoriel de [vec]U[/vec] par [vec]V [/vec], noté [vec]U[/vec] ∧ [vec]V [/vec], est le vecteur [vec]W[/vec] tel que :

• [vec]W[/vec] ⊥ [vec]U[/vec]    et    [vec]W[/vec] ⊥ [vec]V[/vec].
• Les vecteurs [vec]U[/vec], [vec]V[/vec] et [vec]W[/vec], pris dans cet ordre, forment un trièdre direct.
• [mod][vec]W[/vec][/mod] = [mod][vec]U[/vec][/mod] × [mod][vec]V[/vec][/mod] × [bar]sin α[/bar]

Propriétés

• [vec]U[/vec] ∧ [vec]V[/vec] = [vec]0[/vec]    si    [vec]U[/vec] // [vec]V[/vec]    ou    [vec]U[/vec] = [vec]0[/vec]    ou    [vec]V [/vec] = [vec]0[/vec].
• [vec]U[/vec] ∧ [vec]V[/vec] = - [vec]V [/vec] ∧ [vec]U[/vec]    Le produit vectoriel n'est pas commutatif.
• [mod][vec]W[/vec][/mod] = [mod][vec]U[/vec][/mod] × [mod][vec]V [/vec][/mod]    si    [vec]U[/vec] ⊥ [vec]V [/vec]

Expression analytique

Si    [vec]U[/vec] (u₁; u₂; u₃)    et    [vec]V[/vec] (v₁; v₂; v₃)    alors    [vec]U[/vec] ∧ [vec]V[/vec] (u₂.v₃-u₃.v₂ ; u₃.v₁-u₁.v₃ ; u₁.v₂-u₂.v₁)

Il existe plusieurs manières d'effectuer un produit vectoriel. La méthode proposée ci-dessous prend comme exemple [vec]U[/vec] ( 2; 3; 4 ) et [vec]V[/vec] ( 5; 6; 7 ). Le résultat à trouver est [vec]U[/vec] ∧ [vec]V[/vec] ( -3; 6; -3 ).

Les étapes à suivre sont les suivantes :

1. On écrit les coordonnées des vecteurs les unes en dessous des autres.
2. On recopie les deux premières lignes et on barre la première ligne.
3. On effectue des produits en croix avec une soustraction.
   • Les deux premières lignes permettent de calculer la coordonnée en x.
   • Les deux lignes du milieu la coordonnée en y.
   • Et les deux dernières lignes la coordonnée en z.