En construction mécanique, il est fréquent de devoir adapter le mouvement engendré par un actionneur, réduire la fréquence de rotation ou convertir une rotation en une translation, par exemple. On distingue habituellement :
Une pièce qui fait bouger une autre pièce qui en entraîne une autre forme une chaîne de pièces en mouvement, autrement dit une chaîne cinématique. Elle se caractérise par :
Un mouvement de rotation est plus ou moins rapide.
Très souvent en mécanique, il faut transformer des tr/min en rad/s ou inversement. On utilise les relations :
ω = [div]π . N[sur]30[/div] ou N = [div]30 . ω[sur]π[/div]
ω : Vitesse angulaire en rad/s.
N : Fréquence de rotation en tr/min.
Le rapport de transmission r est le rapport entre la vitesse de sortie (celle du récepteur) et la vitesse d'entrée (celle du moteur).
r = [div]Nsortie[sur]Nentrée[/div] = [div]ωsortie[sur]ωentrée[/div]
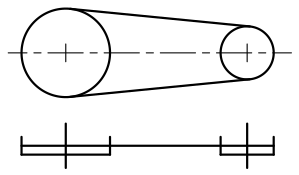
Ces systèmes permettent de transmettre des mouvements de rotation entre des axes éloignés.
Il existe plusieurs sortes de courroies :




En fonctionnement, les systèmes poulies - courroies plates ou trapézoïdales admettent un léger glissement, entre la poulie et la courroie. De ce fait, le rapport de transmission est approximatif. Le diamètre primitif de la poulie est le diamètre du cercle passant par le centre géométrique de la courroie. Le rapport des vitesses de rotation est inversement proportionnel au rapport des diamètres primitifs des poulies.
r = [div]Nsortie[sur]Nentrée[/div] = [div]ωsortie[sur]ωentrée[/div] ≈ [div]dentrée[sur]ωsortie[/div]
dentrée, dsortie : Diamètres primitifs des poulies.
Les systèmes poulies - courroie crantée ou roues dentées - chaîne, du fait de l'absence de glissement, offrent un rapport de transmission rigoureux. Le rapport des vitesses de rotation est inversement proportionnel au rapport des nombres de dents.
r = [div]Nsortie[sur]Nentrée[/div] = [div]ωsortie[sur]ωentrée[/div] = [div]Zentrée[sur]Zsortie[/div]
Zentrée, Zsortie : Nombres de dents des poulies crantées ou des roues dentées.
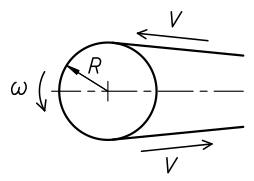
Elle se calcule avec la relation :
V = R . ω
V : Vitesse de translation de la courroie ou de la chaîne en m/s.
R : Rayon primitif de la poulie ou de la roue en m.
ω : Vitesse angulaire de la poulie ou de la roue dentée en rad/s.

Les engrenages permettent de transmettre des mouvements de rotation entre des axes relativement proches. On distingue :
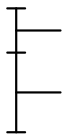
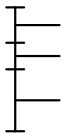
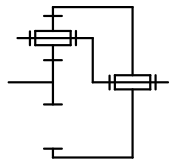
Un engrenage peut être :
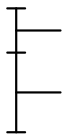
La denture d'une roue peut être :

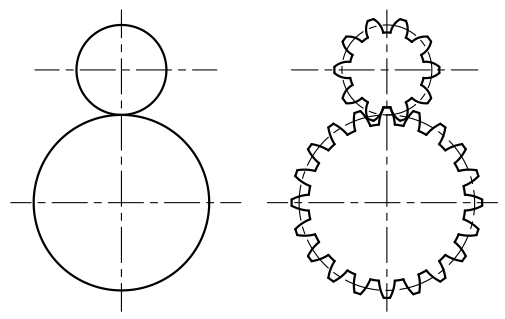
Les cylindres primitifs sont les cylindres de frictions de même entraxe qui donneraient le même rapport de transmission que l'engrenage.
Le pas p d'une roue dentée est la longueur de l'arc de cercle primitif compris entre deux profils de denture consécutifs. C'est aussi la distance entre deux dents de la crémaillère qui engrène avec la roue.
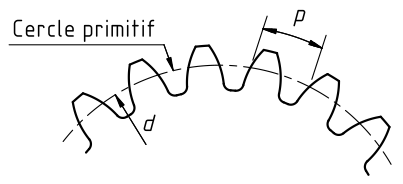
Le module m se définit avec la relation :
p = π . m
Presque toutes les dimensions d'une roue dentée sont définies à partir du module. Deux roues dentées ne peuvent engrener que si elles ont même module.

Les modules sont normalisés et prennent les valeurs suivantes :
0,5 - 0,6 - 0,8 - 1 - 1,25 - 1,5 - 2 - 2,5 - 3 - 4 - 5 - 6 - 8 - 10
Le diamètre primitif d d'une roue dentée se calcule avec la relation :
d = m . Z
p : Pas en mm.
d : Diamètre primitif en mm.
m : Module en mm.
Z : Nombre de dents de la roue.
Les points de contact entre les dents de deux roues dentées qui engrènent sont toujours situés sur la même droite, la ligne d'action. Pour un engrenage normalisé, la ligne d'action est inclinée de 20°. Si on néglige les frottements, l'action d'une roue dentée sur une autre a pour résultante une force inclinée de 20°.
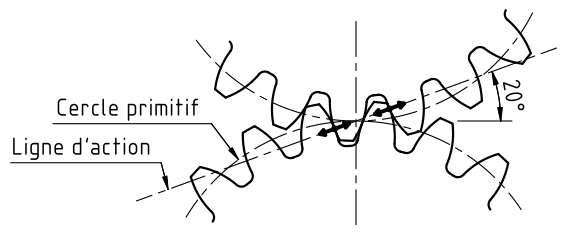
Le cercle tangent à la ligne d'action se nomme le cercle de base. Le profil de denture est une développante ce cercle partant du cercle de base.
Soient deux roues dentées qui engrènent. Le rapport des vitesses de rotation est inversement proportionnel au rapport des nombres de dents des roues.
r = [div]Nsortie[sur]Nentrée[/div] = [div]ωsortie[sur]ωentrée[/div] = [div]Zentrée[sur]Zsortie[/div]
Nentrée, Nsortie : Fréquences de rotation des roues en tr/min.
ωentrée, ωsortie : Vitesses angulaires des roues en rad/s.
Zentrée, Zsortie : Nombres de dents des roues.
Une roue qui en entraîne une autre est dite menante. Une roue entraînée par une autre est dite menée. On montre que le rapport de transmission se calcule avec la relation ci-dessous.
r = [div]Produit des nombres de dents des roues menantes[sur] Produit des nombres de dents des roues menées[/div]
Dans un train d'engrenages, il arrive que certaines roues soient à la fois menantes et menées. Ces roues sont généralement utilisées pour changer le sens de rotation des roues, parfois pour augmenter la distance entre deux axes.
Dans l'exemple ci-dessous, l'axe du moteur est lié à la roue dentée 1 :
Le rapport de transmission se calcule avec la relation :
r = [div]Z1 . Z3 . Z4[sur] Z2 . Z4 . Z5[/div] = [div]Z1 . Z3[sur] Z2 . Z5[/div]

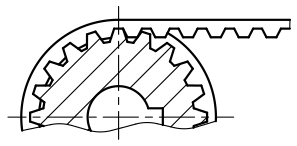
Le système roue et vis sans fin permet d'obtenir un rapport de vitesses important pour un faible encombrement. Son rendement est médiocre du fait de l'importance des frottements.
Si la vis sans fin comporte un seul filet, le système est (presque toujours) irréversible, c'est à dire que la vis sans fin peut entraîner la roue mais pas l'inverse. Cette propriété est intéressante pour certains mécanismes, comme les treuils. Si la vis sans fin comporte trois filets, le système est généralement réversible.
Le système roue - vis sans fin se comporte comme un engrenage. La vis sans fin est une roue à denture hélicoïdale dont le nombre de dents est égal au nombre de filets de la vis.
Les trains épicycloïdaux autorisent de grands rapports de réduction pour un faible encombrement. Ils se calculent avec la formule de Willis.
L'exemple de train épicycloïdal schématisé ci-dessous comporte :
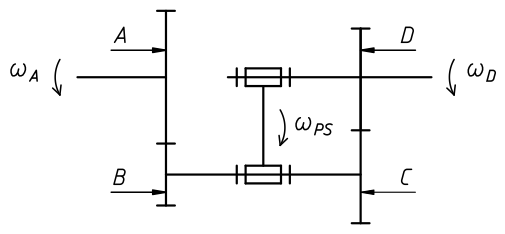
Formule de Willis : r = [div]ωD - ωPS[sur]ωA - ωPS[/div]
La raison r est le rapport de transmission si on considère le bras porte satellite immobilisé, multiplié par -1 si les arbres des planétaires tournent en sens inverse.
Pour cet exemple : r = [div]ZA . ZC[sur]ZB . ZD[/div]
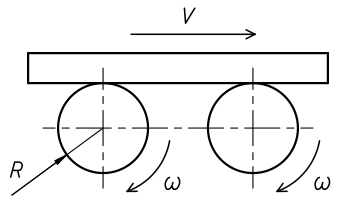
Dans l'exemple d'une pièce posée sur des galets et entraînée par ceux-ci, la vitesse de la pièce se calcule avec la relation :
V = R . ω
V : Vitesse de la pièce en m/s.
R : Rayon des galets en m.
ω : Vitesse angulaire des galets en rad/s.
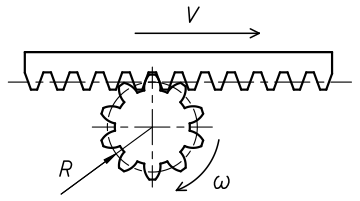
Pour le système pignon - crémaillère, la relation utilisée est similaire, le rayon du galet est remplacé par le rayon primitif du pignon :
V = R . ω
V : Vitesse de la crémaillère en m/s.
R : Rayon primitif du pignon en m.
ω : Vitesse angulaire du pignon en rad/s.
Deux fonctionnements sont possibles :
Dans les deux cas, on utilise la relation : V = [div]p . n . N[sur]60[/div]
V : Vitesse de l'écrou (ou de la vis) en m/s.
p : Pas de la vis en m.
n : Nombre de filets de la vis.
N : Fréquence de rotation de la vis (ou de l'écrou) en tr/min.
Naturellement, il existe d'autres systèmes pour transformer un mouvement de rotation en mouvement de translation :
Les caractéristiques d'une chaîne cinématique se déterminent à partir des caractéristiques cinématiques de chaque constituant.
Dans le servomoteur schématisé ci-dessous, le moteur électrique entraîne un engrenage. L'arbre de sortie de l'engrenage engendre un mouvement de translation à l'aide d'un système vis-écrou.

1er constituant, l'engrenage : ω2 = ω1 . [div]Z1[sur]Z2[/div]
2ème constituant, le système vis-écrou : V = ω2 . [div]n . p[sur]2 . π[/div]
On en déduit : V = ω1 . [div]Z1 . n . p[sur]Z2 . 2 . π[/div]