

Les liaisons entre les pièces d'un mécanisme font intervenir des jeux et des serrages nécessaires à leur fonctionnement. Certaines surfaces doivent avoir une faible rugosité, par exemple pour éviter une usure prématurée. De manière générale, les conditions fonctionnelles engendrent, pour chaque pièce, trois types de contraintes.
cotation dimensionnelle.
cotation géométrique(macrogéométrique).
cotation des états de surface(microgéométrique).

Ces contraintes sont indiquées sur les dessins de définition. Nous nous intéressons, ici, à la cotation dimensionnelle.
dimensions'obtient avec un instrument de mesure. Elle est connue avec une précision qui dépend de l'instrument.
coteindique l'ensemble des dimensions possibles entre deux surfaces. Elle comporte une cote nominale suivie de la tolérance. Elle est inscrite sur un dessin de définition.
La tolérance peut être :


Une tolérance chiffrée
comporte les valeurs des écarts inférieur et supérieur, inscrites l'une en dessous de l'autre.
Une tolérance normalisée
selon le système ISO comporte une (parfois deux) lettre et un nombre.
La lettre, majuscule pour un alésage (ou un contenant) et minuscule pour un arbre (ou un contenu),
indique la position de la tolérance.
Le nombre indique la qualité (ou la valeur) de la tolérance.
Les valeurs des écarts inférieur et supérieur peuvent de calculer ou se retrouver dans un tableau.

La différence entre les dimensions maximale et minimale fixées par la cote
se nomme intervalle de tolérance
.
IT = dimension maxi - dimension mini
L'objectif est de choisir les cotes pour un assemblage de deux pièces.
Dans l'exemple d'une liaison pivot-glissant réalisée avec un arbre et un alésage, si le diamètre de l'arbre est trop grand, il ne rentrera pas dans l'alésage. Et s'il est trop petit, le jeu sera très important. Les diamètres de l'arbre et de l'alésage doivent être similaires, le diamètre de l'alésage restant légèrement supérieur à celui de l'arbre.
Un ajustement
est le degré de jeu ou de serrage dans un assemblage de deux pièces.
Il se caractérise par une dimension nominale commune aux deux pièces.
Une des pièces est le contenant, par exemple un alésage.
L'autre pièce est le contenu, par exemple un arbre.
Le respect des cotes sur les pièces assure leur interchangeabilité.
Soient deux pièces 1 et 2 s'emboîtant l'une dans l'autre. Ci-dessous, la pièce 1 est le contenant et la pièce 2 le contenu.

L'ensemble des dimensions possibles pour d1 et d2 sont définies par les cotes C1 et C2.

Le jeu ou le serrage entre les pièces 1 et 2 peut être plus ou moins important. Il dépend des dimensions limites définies par les cotes C1 et C2.
Il existe trois types d'ajustement :
| Type d'ajustement | Caractéristiques | Cas d'emploi |
|---|---|---|
| Avec Jeu | J maxi > 0 et J mini > 0 | Pièces mobiles entre elles |
| Incertain | J maxi > 0 et J mini < 0 | Pièces immobiles entre elles |
| Avec serrage | J maxi < 0 et J mini < 0 |
Les ajustements sont normalisés et sont choisis selon le fonctionnement souhaité.
| Cas d'emploi | Ajustements classiques | |
|---|---|---|
| Pièces mobiles entre elles | Grand jeu | H11/d11 |
| Jeu usuel | H9/e9, H8/e8 | |
| Jeu précis | H7/g6 | |
| Pièces immobiles entre elles | Mise en place au maillet | H7/m6 |
| Mise en place à la presse | H7/p6 | |
Un ajustement peut être indiqué sur le dessin d'ensemble. On écrit la dimension nominale commune, suivie des tolérances normalisées sur chaque pièce, en commençant par celle du contenant.

Les cotes issues de l'ajustement sont reportées sur les dessins de définition.

L'objectif est de choisir les cotes pour un assemblage de plusieurs pièces.
Dans l'exemple ci-dessous, si la rondelle est trop épaisse, l'anneau élastique ne pourra être monté. L'épaisseur de la rondelle doit toutefois être suffisante pour éviter un jeu trop important.

Une condition fonctionnelle
est une nécessité dimensionnelle
assurant le montage ou le fonctionnement correct d'un mécanisme.
Elle est représentée sur le dessin d'ensemble par le vecteur condition,
dessiné par une double flèche.
Par convention, ce vecteur est orienté de la gauche vers la droite
ou du bas vers le haut.
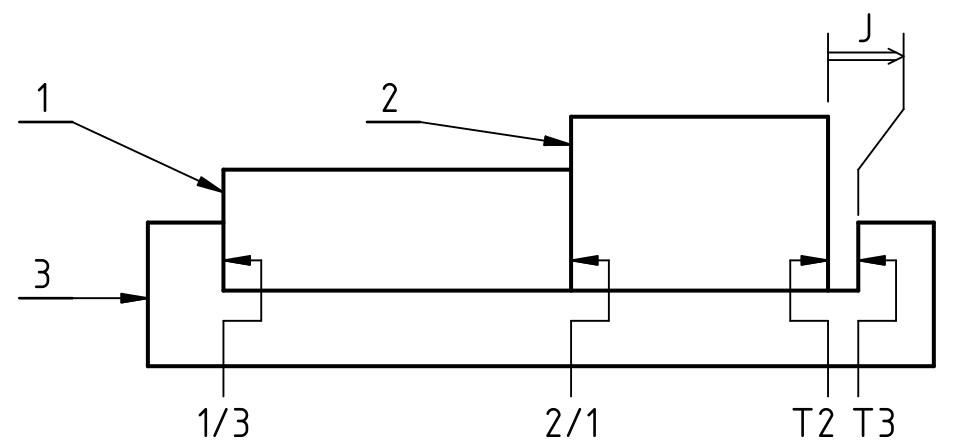
Dans l'exemple ci-dessous, on souhaite pouvoir placer ou retirer deux pièces 1 et 2 d'une boîte 3,
sans qu'aucune des pièces ne soient jamais bloquées.
Ceci est possible si, en poussant les pièces 1 et 2 vers la gauche, il subsiste un faible jeu, représenté par le vecteur J sur le dessin.
J est la cote condition
ou le vecteur condition
.

Bien qu'il s'agisse d'un vecteur, on ne place habituellement pas de flèche au-dessus du caractère J, comme c'est le cas en mathématique.
Ce vecteur est délimité par deux surfaces T2 et T3 dites terminales
.
Les surfaces 1/2 et 1/3, communes au pièces 1 et 2 d'une part, 1 et 3 d'autre part, sont des surfaces de contact
.
Dans cette chaîne de contacts unidirectionnelle, les surfaces terminales et les surfaces de contact sont dites fonctionnelles
.
Le graphe des contacts
ou graphe des surfaces de contacts perpendiculaires à la cote condition
peut aider à établir la chaîne de cotes.
Quand il comporte plusieurs boucles, la boucle la plus courte met en évidence
les pièces concernées par la chaîne de cotes minimale. Ce graphe comporte :
Pour l'exemple précédent :

Dans l'exemple ci-dessous, les pièces 1 et 3 ne sont pas en contact. Elles ont pourtant une surface commune, indiquée en trait interrompu sur le graphe.

L'ensemble des cotes C1, C2, ... Cn nécessaires et suffisantes au respect de la cote condition J est appelée chaîne de cotes
.
Chaque cote, représentée par un vecteur, est également appelée vecteur cote
, cote orientée
ou maillon de la chaîne de cotes
.
Chaque cote de la chaîne étant relative à une pièce, elle commence et se termine sur la même pièce.
J = C1 + C2 + ... + Cn
Pour un vecteur cote condition donné, la chaîne de cotes minimale est celle qui comporte le nombre le plus réduit de cotes. Dans une chaîne de cotes minimale, il ne peut y avoir qu'une cote par pièce.
On montre que l'intervalle de tolérance de la cote condition est égal à la somme des intervalles de tolérance de chaque maillon de la chaîne de cotes.
IT J = IT C1 + IT C2 + ... + IT Cn
Pour reprendre l'exemple précédent :
J = C1 + C2 + C3.
Il s'agit ici d'un relation vectorielle : C1, C2 et C3 sont les vecteurs cotes dont dépend J.
On peut aussi écrire :

A partir des deux relations précédentes :
J maxi - J mini = (C3 maxi - C3 mini) + (C1 maxi - C1 mini) + (C2 maxi - C2 mini) ⇒
IT J = IT C1 + IT C2 + IT C3