La cinématique est la partie de la mécanique où l'on étudie les mouvements des solides, indépendamment des causes qui les produisent.
Tout est relatif, disait Einstein. Un mouvement se définit toujours par rapport à un référentiel. Par exemple, un voyageur dans un train est immobile par rapport au train, mais se déplace par rapport à la gare. Le train et la gare sont deux référentiels différents.
Lors d'une étude de cinématique, les grandeurs recherchées sont les positions, les vitesses et les accélérations. Ces grandeurs varient au cours du temps.
Deux mouvements nous intéressent particulièrement :
Le mouvement de translation rectiligne, ou plus simplement mouvement rectiligne, est celui réalisé par une liaison glissière. On distingue :
Le mouvement de rotation autour d'un axe fixe, ou plus simplement mouvement circulaire, est celui réalisé par une liaison pivot. On distingue :
Un référentiel est un solide ou un ensemble de solides immobiles les uns par rapports aux autres, servant de référence pour l'étude des mouvements. Considérons un solide dont le mouvement est étudié par rapport à un solide de référence.
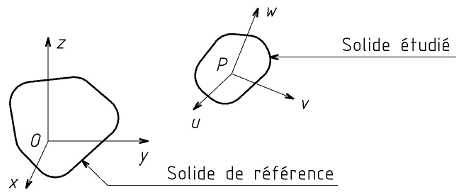
Les douze coordonnées du point P et celles des vecteurs
Un paramètre est une distance ou un angle permettant de définir simplement
la position d'un solide par rapport à un référentiel.
Pour un mouvement rectiligne ou circulaire, connaître la position d'un point lié au solide est suffisant
pour connaître celle du solide. Soit
(O;
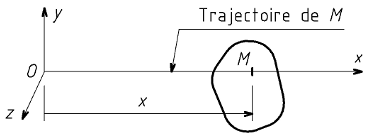
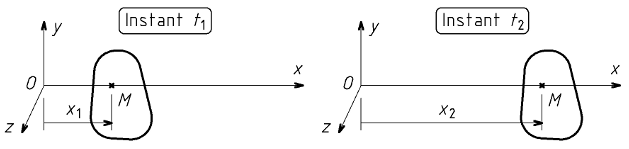
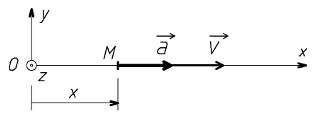
Plaçons l'axe (Ox) sur la trajectoire du point M. Le paramètre définissant la position du solide étudié est l'abscisse x du point M. L'abscisse x varie au cours du temps.
Plaçons l'axe (Oz) sur l'axe de rotation et le point O au centre de la trajectoire du point M. Le paramètre définissant la position du solide étudié est l'angle orienté θ entre l'axe (Ox) et la droite (OM), autrement dit l'abscisse angulaire du point M. L'abscisse angulaire θ varie au cours du temps.

La trajectoire d'un point est la courbe passant par les positions occupées par ce point au cours du temps.
Pour un mouvement rectiligne, les trajectoires des points liés au solide étudié sont des droites parallèles.
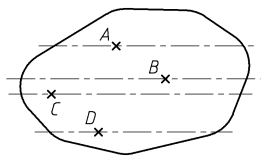
Pour un mouvement circulaire, les trajectoires des points liés au solide étudié sont des cercles dont les centres sont situés sur l’axe de rotation.
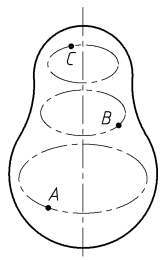
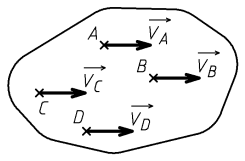
Pour un mouvement rectiligne, tout point lié au solide étudié à la même vitesse, représentée par le même vecteur.
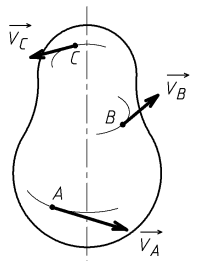
Pour un mouvement circulaire, les vecteurs vitesses sont tangents aux trajectoires. Les normes de ces vecteurs sont proportionnelles aux rayons des trajectoires.
Un mouvement peut se décomposer en plusieurs phases. Chaque phase du mouvement, uniforme ou uniformément varié, s'étudie alors séparément.
Dans le repère fixe
(O;
La vitesse du point M peut varier au cours du temps. Au cours d'une phase, la représentation graphique de la vitesse en fonction du temps est un segment de droite. A l'instant t1, la vitesse du point M est V1 et à l'instant t2, sa vitesse est V2.
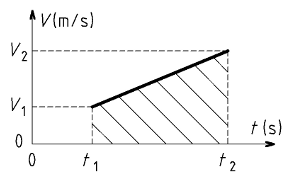
Le déplacement du point M entre les instants t1 et t2, en m, est le produit de la vitesse moyenne par la durée.
Δx = Vmoy . Δt ⇒
x2 - x1 =
L'accélération du point M, en m/s2, est égale à la variation de la vitesse divisée par la durée.
∂ =
Dans le repère fixe
(O;
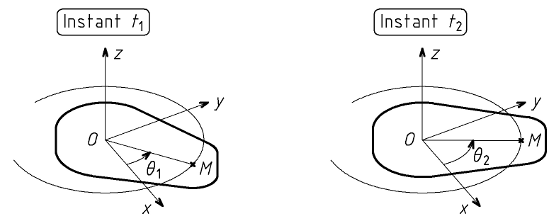
La vitesse angulaire du point M peut varier au cours du temps. Au cours d'une phase, la représentation graphique de la vitesse angulaire en fonction du temps est un segment de droite. A l'instant t1, la vitesse angulaire du point M est ω1 et à l'instant t2, sa vitesse angulaire est ω2.
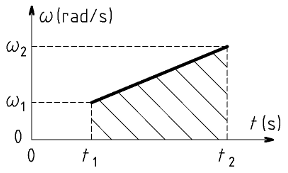
Le déplacement angulaire du point M entre les instants t1 et t2, en rad, est le produit de la vitesse angulaire moyenne par la durée.
Δθ = ωmoy . Δt ⇒
θ2 - θ1 =
L'accélération angulaire du point M, en rad/s2, est égale à la variation de la vitesse angulaire divisée par la durée.
Ω =
Le mouvement d'un point se caractérise par :
Sur la trajectoire du point M, ayant choisi une origine Mo et un sens positif,
l'abscisse curviligne s du point M est égale
à la valeur algébrique de l'arc orienté MoM.
L'abscisse curviligne s varie au cours du temps.
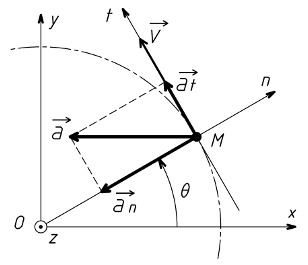
La vitesse du point M est représentée par le vecteur vitesse

La vitesse V du point M, en m/s, se calcule avec la relation :
V = s' =
L'accélération tangentielle ∂t du point M, en m/s2, se calcule avec la relation :
∂t = V' =
Soit
(O;
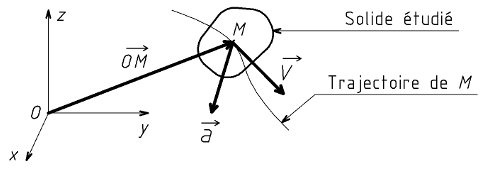
Soient x, y et z les coordonnées du vecteur
L'abscisse x, en m, définit la position du point M.
La vitesse V, en m/s, est la variation d'abscisse par unité de temps.
L'accélération ∂, en m/s2, est la variation de vitesse par unité de temps.
L'abscisse angulaire θ, en rad, définit la position du point M.
θ = (
La vitesse angulaire ω, en rad/s, est la variation d'abscisse angulaire par unité de temps.
ω = θ' =
L'accélération angulaire Ω, en rad/s2, est la variation de vitesse angulaire par unité de temps.
Ω = ω' =
Soient le vecteur unitaire
La position du point M, dont la trajectoire est le cercle de centre O et de rayon R = OM, s'écrit avec la relation ci-dessous.
La vitesse
Exprimée en m/s, elle se calcule avec la relation :
V = R . ω
L'accélération
Exprimées en m/s2, elles se calculent avec les relations :
∂n =
∂t =
Une manière assez générale de résoudre un problème de cinématique consiste :
Dès que les équations horaires sont connues, il devient aisé de répondre à n'importe quelle question concernant les caractéristiques de ces points.
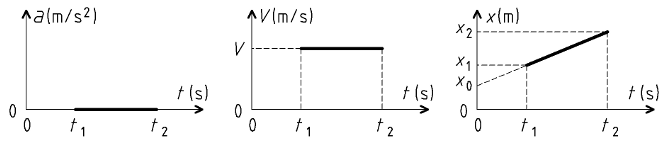
Cette équation est de la forme :
∂ = 0
Cette équation est de la forme :
V = V0
Déterminer l'équation horaire consiste à trouver la valeur de la constante V0.
Cette équation est de la forme :
x = V . t + x0
Déterminer l'équation horaire consiste à trouver les valeurs des constantes V et x0.
On peut aussi écrire, pour éviter le calcul de x0 :
x = V . (t - ti) + xi
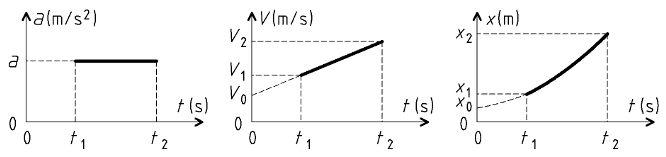
Cette équation est de la forme :
∂ = ∂0
Déterminer l'équation horaire consiste à trouver la valeur de la constante ∂0.
Cette équation est de la forme :
V = ∂ . t + V0
Déterminer l'équation horaire consiste à trouver les valeurs des constantes ∂ et V0.
On peut aussi écrire, pour éviter le calcul de V0 :
V = ∂ . (t - ti) + Vi
Cette équation est de la forme :
x = ∂ .
Elle s'obtient en recherchant une primitive de la vitesse :
V = x' = ∂ . t + V0
Déterminer l'équation horaire consiste à trouver les valeurs des constantes ∂, V0 et x0.
On peut aussi écrire, pour éviter le calcul de x0 :
x = ∂ .
Cette équation est de la forme :
Ω = ω' = 0
Cette équation est de la forme :
ω = ω0
Déterminer l'équation horaire consiste à trouver la valeur de la constante ω0.
Cette équation est de la forme :
θ = ω . t + θ0
Déterminer l'équation horaire consiste à trouver les valeurs des constantes ω et θ0.
On peut aussi écrire, pour éviter le calcul de θ0 :
θ = ω . (t - ti) + θi
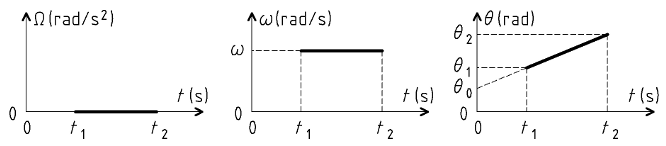
Cette équation est de la forme :
Ω = ω' = Ω0
Déterminer l'équation horaire consiste à trouver la valeur de la constante Ω0.
Cette équation est de la forme :
ω = Ω . t + ω0
Déterminer l'équation horaire consiste à trouver les valeurs des constantes Ω et ω0.
On peut aussi écrire, pour éviter le calcul de ω0 :
ω = Ω . (t - ti) + ωi
Cette équation est de la forme :
θ = Ω .
Elle s'obtient en recherchant une primitive de la vitesse angulaire :
ω = θ' = Ω . t + ω0
Déterminer l'équation horaire consiste à trouver les valeurs des constantes Ω, ω0 et θ0.
On peut aussi écrire, pour éviter le calcul de θ0 :
θ = Ω .
