CINEMATIQUE
MOUVEMENTS PLANS

Introduction

L'étude des mouvements plans s'intéresse essentiellement aux vitesses et aux trajectoires des points, les vitesses étant tangentes aux trajectoires. La cinématique plane, s'appuyant sur de nombreux tracés, se nomme communément cinématique graphique. Le mouvement d'un solide 1 se définit par rapport à un solide de référence 2. La vitesse d'un point M lié au solide 1 par rapport au solide 2 se note V_{M 1/2}.

Plusieurs points liés à un même solide

Pour étudier les mouvements de plusieurs points, liés à un même solide en mouvement par rapport à un solide de référence, on utilise :

• La méthode du CIR.
• Ou celle de l'équiprojectivité.

Un seul point lié à plusieurs solides

Pour étudier les mouvements d'un unique point, lié à divers solides en mouvement les uns par rapports aux autres, on utilise la relation de composition des vecteurs vitesse.

Points coïncidant à un instant donné

La cinématique s’intéresse, pour une bonne part, au mouvement du point, mais il faut remarquer qu’il s’agit du point géométrique et non du point matériel. Cela signifie qu'un point lié à un solide peut éventuellement être situé en dehors de ce solide.

Deux points étudiés, liés à deux solides en mouvement, peuvent occuper la même position à un instant donné. On dit que ces points coïncident.

Exemple

Considérons une carrosserie, une roue de voiture et une route comme trois solides distincts. Ci-dessous :

• Le mouvement de la roue 3 par rapport à la carrosserie 1 est une rotation de centre B.
• Le mouvement de la carrosserie 1 par rapport à la route 2 est une translation horizontale.
• La roue 3 roule sans glisser sur la route 2.

Par conséquent :

• La trajectoire T_A∈3/1 du point A lié à la roue 3 par rapport à la carrosserie 1 est le cercle de centre B et de rayon AB.
• La trajectoire T_A∈1/2 du point A lié à la carrosserie 1 par rapport à la route 2 est la droite horizontale passant par A.
• La trajectoire T_A∈3/2 du point A lié à la roue 3 par rapport à la route 2 est la cycloïde représentée sur le dessin.

Le point A lié à la carrosserie 1 et le point A lié à la roue 3 coïncident à l'instant de l'étude.

Types de mouvements plans

Un solide est en mouvement plan si chaque point lié à ce solide se déplace dans un plan. Un mouvement plan peut être :

• Un mouvement de translation rectiligne.
• Un mouvement de translation circulaire.
• Un mouvement de translation quelconque (ou curviligne).
• Un mouvement de rotation (autour d'un axe fixe).
• Un mouvement plan quelconque.

Ci-dessous, un exemple de translation circulaire : Les nacelles du manège tournent en conservant la même orientation.

On montre qu'un mouvement plan quelconque est équivalent à un mouvement de rotation dont le centre de rotation se déplace. Ce centre de rotation se nomme centre instantané de rotation ou CIR. A l'instant de l'étude, le solide étudié se comporte comme s'il tournait autour du CIR. On notera que le CIR est le seul point du solide dont la vitesse est nulle.

Centre instantané de rotation

Mouvement plan quelconque

Soit deux points A et B liés à un même solide 1 en mouvement par rapport à un solide 2. Les supports des vecteurs vitesse V_{A 1/2} et V_{B 1/2} sont supposés connus et non parallèles.

• La droite passant par A et perpendiculaire au support de V_{A 1/2} coupe la droite passant par B et perpendiculaire au support de V_{B 1/2}, en un point I : Ce point est le CIR_1/2. A l'instant de l'étude, le solide se comporte comme s'il tournait autour du point I.
  
• La vitesse V_{A 1/2} étant connue, on peut calculer la vitesse instantané de rotation ω_1/2 avec la relation : V_{A 1/2} = IA . ω_1/2
• La vitesse d'un point B quelconque se détermine alors sachant que :
  • V_{B 1/2} est perpendiculaire à (IB).
  • Le sens de V_{B 1/2} est donné par le sens de rotation du solide.
  • V_{B 1/2} = IB . ω_1/2

On peut calculer la vitesse V_{B 1/2}, mais on peut également l'obtenir par un tracé. En disposant d'un rapporteur, on mesure l'angle α après avoir tracé V_{A 1/2} en respectant l'échelle choisie. On reporte ensuite l'angle α pour tracer V_{B 1/2}. On détermine enfin V_{B 1/2} en mesurant la longueur du vecteur correspondant et en tenant compte de l'échelle du tracé.

Si on dispose d'un compas, on peut placer le point B' sur la droite (IA) de telle sorte que IB = IB'. On trace ensuite le vecteur V_{B' 1/2}. Les normes des vecteurs V_{B' 1/2} et V_{B 1/2} sont égales.

La méthode du CIR est inutilisable si le CIR est situé en dehors de la feuille sur laquelle sont effectués les tracés.

Mouvements particuliers

Mouvement de translation

Le mouvement de translation est le cas particulier où le CIR est situé à une distance infinie du solide étudié. Les vecteurs vitesse de chaque point du solide sont identiques.

Mouvement de rotation

Pour un mouvement de rotation d'un solide 1 autour d'un axe fixe lié à un solide 2 :

• Les trajectoires des points liées au solide étudié sont des cercles dont les centres sont situés sur l'axe de rotation.
• Les vitesses sont tangentes aux trajectoires. Si, par exemple, la trajectoire d'un point A est un cercle de centre O, alors le vecteur vitesse V_{A 1/2} est perpendiculaire à la droite (OA).
• La vitesse du point A se calcule avec la relation : V_{A 1/2} = OA . ω_1/2
  V_{A 1/2} : Vitesse du point A en m/s.
  OA : Rayon de la trajectoire en m.
  ω_1/2 : Vitesse de rotation en rad/s.

Le mouvement de rotation est un mouvement plan dont le CIR reste fixe.

Equiprojectivité

La résolution d'un problème de cinématique plane se fait souvent graphiquement. La position du CIR est parfois située en dehors de la feuille sur laquelle est dessiné le solide étudié. On utilise alors la méthode de l'équiprojectivité.

On montre que pour deux points A et B liés à un même solide 1 en mouvement par rapport à un solide 2, les projections orthogonales de V_{A 1/2} et de V_{B 1/2} sur la droite (AB) sont deux vecteurs identiques.

Dans l'exemple ci-dessous, on a donc : AK = BL

La méthode de l'équiprojectivité est inutilisable si la projection orthogonale du vecteur vitesse donne le vecteur nul. Et si cette projection est de faible longueur, les tracés donneront des résultats peu précis...

Composition des vitesses

Exemples

Voyageur marchant sur un wagon en mouvement

Prenons l'exemple d'un voyageur 1 marchant sur un wagon 2 en mouvement par rapport à une gare 3. La vitesse du voyageur 1 par rapport à la gare 3 est celle du train 2 par rapport à la gare 3 à laquelle s'ajoute la vitesse du voyageur 1 par rapport au train 2.

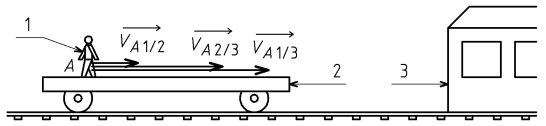
Si le voyageur est situé au point A, alors :

V_{A 1/3} = V_{A 1/2} + V_{A 2/3}

Les vitesses étant horizontales, sous forme vectorielle, on obtient :

V_{A 1/3} = V_{A 1/2} + V_{A 2/3}

Bateau traversant un fleuve

On montre que la relation précédente est vrai aussi pour des vecteurs non parallèles. Ci-dessous, un bateau 1 représenté en vue de dessus tente de traverser un fleuve 2, dont le courant par rapport à la berge 3 n'est pas négligeable. La vitesse du bateau 1 par rapport à la berge 3 est égale à la somme vectorielle de la vitesse du bateau 1 par rapport au fleuve 2 et de la vitesse du fleuve 2 rapport à la berge 3.

Pour un point A lié au bateau :

V_{A 1/3} = V_{A 1/2} + V_{A 2/3}

Cas général

Dans le cas général, quels que soient trois solides 1, 2 et 3 et un point M :

V_{M 1/2} = V_{M 1/3} + V_{M 3/2}

Cette relation se nomme relation de composition des vecteurs vitesse.

Remarque

V_{M 1/2} = - V_{M 2/1}

Les deux vecteurs vitesse sont directement opposés. Ils ont le même support.

Mouvement relatif au contact entre deux solides

Roulement sans glissement entre deux solides

Exemple

Considérons une roue 1 roulant sans glisser sur une route 2. Sur le schéma ci-dessous, la trajectoire d'un point lié à la roue est représentée.

Au point A, la trajectoire admet une tangente verticale.

• Juste avant le point A, la vitesse du point étudié, lié à la roue, est dirigée vers le bas.
• Juste après le point A, cette vitesse est dirigée vers le haut.

Pour qu'une vitesse change de sens tout en conservant la même direction (verticale dans le cas présent), il est nécessaire que cette vitesse soit nulle à un instant donné. Intuitivement, on conclue que la vitesse au point A est nulle.

Cas général

D'une manière générale, si deux solides 1 et 2, en contact ponctuel, A étant le point de contact, roulent sans glisser l'un sur l'autre alors :

• A est le CIR_1/2.
• V_{A 1/2} = 0.

Glissement entre deux solides

Soient :

• Deux solides 1 et 2 en contact ponctuel.
• A le point de contact.
• P le plan tangent commun aux deux solides.

Si le solide 1 glisse sur le solide 2, alors la direction de V_{A 1/2} est parallèle au plan P.