CINETIQUE

Introduction

La cinétique est la partie de la mécanique où l'on étudie les mouvements des solides, en prenant en compte les masses et les inerties. Elle permet, entre autres, de définir le torseur cinétique à partir duquel on pourra déterminer le torseur dynamique.

Centre d'inertie

Le centre d'inertie ou centre de masse d'un solide est le point central de toutes les masses. Il est confondu avec le centre de gravité si on admet que le champ de pesanteur est localement constant.

Un solide peut fréquemment se décomposer en n éléments dont on connaît les centres d'inertie G_i et les masses m_i. Soit O un point quelconque. La position du centre d'inertie G du solide se calcule avec la relation ci-dessous.

OG = m₁.OG₁+ m₂.OG₂+...+ m_n.OG_n m₁+m₂+...+m_n

m₁+m₂+...+m_n représente la masse totale du solide. Pour des raisons pratiques, le point O est généralement l'origine du repère dans lequel s'écrivent les coordonnées des points G_i.

Moment d’inertie par rapport à un axe

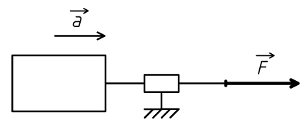
Prenons l'exemple de deux solides, l'un en liaison glissière avec un référentiel fixe, l'autre en liaison pivot. Les liaisons sont parfaites. Pour le mouvement de translation, le principe fondamental de la dynamique permet d'écrire :

F = m . ∂

La force F nécessaire pour déplacer le solide en translation est proportionnelle :

• A la masse m du solide.
• A son accélération ∂.

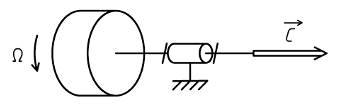
La relation équivalente, pour le mouvement de rotation, s'écrit :

C = J . Ω

La couple C nécessaire pour entraîner le solide en rotation est proportionnel :

• Au moment d'inertie J du solide par rapport à l'axe de rotation.
• A son accélération angulaire Ω.

Le moment d'inertie constitue donc, en quelque sorte, l'équivalent de la masse pour un mouvement de rotation. Il est utilisé en dynamique, mais également pour calculer l'énergie cinétique :

• Cas d'un mouvement de translation : Ec = 12 . m . V ²
• Cas d'un mouvement de rotation : Ec = 12 . J . ω ²

Définition

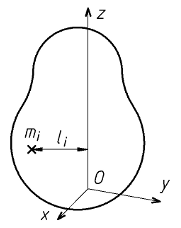
Soit m_i la masse de chaque particule i d'un solide, chaque particule étant située à la distance l_i de l'axe (Oz). Le moment d'inertie du solide par rapport à l'axe (Oz), en kg.m², se calcule avec la relation ci-dessous.

J_Oz = m_i . l_i ²

Considérons les cas suivants :

• Une boule ponctuelle située à la distance R de l'axe (Oz).
• Une barre effilée située à la distance R de l'axe (Oz) et parallèle à cet axe.
• Un anneau fin de rayon R et d'axe (Oz).
• Un tube de faible épaisseur de rayon R et d'axe (Oz).

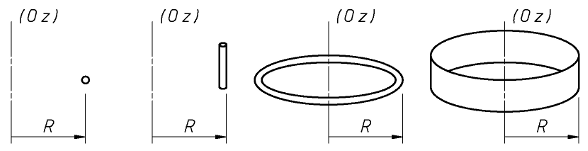
A chaque fois, toute la matière constituant le solide se trouve une distance unique de l'axe (Oz). Les moments d'inertie par rapport à l'axe (Oz) se calculent alors avec la même relation ci-dessous. On note m la masse totale du solide.

J_Oz = m . R²

Moments d'inertie de quelques volumes élémentaires

Pour les solides suivants, de masse m et le centre de masse G, la résolution de l'intégrale donne les résultats ci-dessous.

Cylindre plein		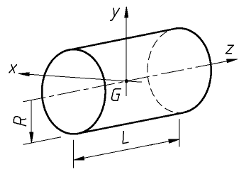JGx = JGy = m . R24 + m . L212 JGz = m . R22
Tube d'épaisseur non négligeable		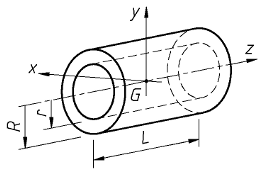JGx = JGy = m . ( R2 + r2 )4 + m . L212 JGz = m . ( R2 + r2 )2
Sphère pleine		JGx = JGy = JGz = 2 . m . R25
Parallélépipède rectangle		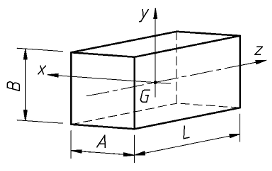JGx = m . ( L2 + B2 )12 JGy = m . ( L2 + A2 )12 JGz = m . ( A2 + B2 )12
Cône plein		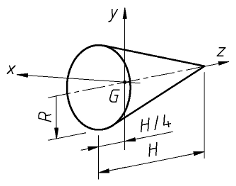JGx = JGy = 3 . m . R220 + 3 . m . H25 JGz = 3 . m . R210

Théorème de Huygens

Soit un solide de masse m et de centre de masse G. Soit d la distance entre l'axe (Oz) et l'axe (Gz).

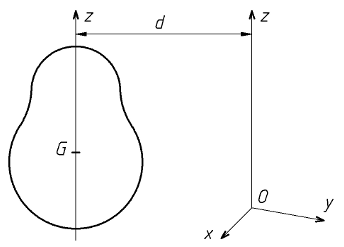
Le moment d'inertie J_Gz étant connu, le moment d'inertie J_Oz se calcule avec la relation :

J_Oz = J_Gz + m . d²

Exemple

Considérons la barre fine de masse m et de longueur L ci-dessous :

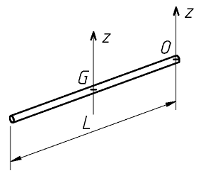
On sais que   J_Gz = m . L²12

En appliquant le théorème de Huygens :

J_Oz = J_Gz + m . (L / 2)² = m . L²12 + m . L²4 = m . L²3

Opérateur d'inertie

Moments d'inertie par rapport à un plan, un axe ou un point

Considérons un solide (S) et un repère orthonormé direct (O; x, y, z ). Chaque particule M_i du solide (S) a pour masse m_i et pour coordonnées x_i, y_i et z_i dans le repère (O; x, y, z ).

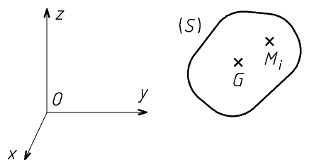
Le moment d'inertie, en kg.m², se calcule par rapport à un plan, un axe ou un point.

Moment d'inertie par rapport au plan (Oxy)

J_Oxy = m_i . z_i²

z_i² est le carrée de la distance entre le point M_i et le plan (Oxy).

Moment d'inertie par rapport à l'axe (Ox)

J_Ox = m_i . ( y_i² + z_i² )

y_i² + z_i² est le carrée de la distance entre le point M_i et l'axe (Ox).

Moment d'inertie par rapport au point O

J_O = m_i . ( x_i² + y_i² + z_i² )

x_i² + y_i² + z_i² est le carrée de la distance entre les points M_i et O.

Propriétés

• Le moment d'inertie est toujours positif ou nul.
• J_O = J_Oxy + J_Oxz + J_Oyz
• J_Ox = J_Oxy + J_Oxz

Produits d'inertie

Le produit d'inertie, en kg.m², se définit par rapport à deux axes.

Produit d'inertie par rapport aux axes (Ox) et (Oy)

P_xy = m_i . x_i . y_i

Propriétés

• P_xy est algébrique.
• Si (Oxy) est un plan de symétrie, alors P_xz = P_yz = 0.
• Si (Oxy) et (Oxz) sont deux plans de symétrie, alors P_xy = P_xz = P_yz = 0.

Opérateur d'inertie

Définition

L'opérateur d'inertie se nomme également matrice d'inertie ou tenseur d'inertie. Il se calcule en un point donné.

J_O = J_Ox
-P_xy
-P_xz   -P_xy
J_Oy
-P_yz   -P_xz
-P_yz
J_Oz

Propriété

Quel que soit le solide (S), il est possible de trouver un repère ( G; x₁, y₁, z₁ ) de sorte que tous les produits d'inertie soient tous nuls. L'opérateur d'inertie s'écrit alors :

J_G = J_Gx1
0
0   0
J_Gy1
0   0
0
J_Gz1

Le point G est le centre d'inertie du solide. Les axes (Gx₁), (Gy₁) et (Gz₁) sont les axes principaux d'inertie. Les moments correspondants sont les moments principaux d'inertie.

Moment d'inertie par rapport à un axe quelconque

Soit une droite Δ passant par O, de vecteur unitaire u.

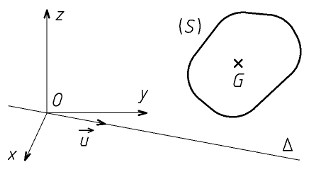
Le moment d'inertie J_Δ du solide (S) par rapport à la droite Δ s'obtient avec la relation :

J_Δ = u . J_O . u

Si a, b et c sont les coordonnées du vecteur u dans le repère (O; x, y, z ), alors :

J_Δ = a². J_Ox + b². J_Oy + c². J_Oz - 2.a.b.P_xy - 2.b.c.P_yz - 2.a.c.P_xz

Torseur cinétique

Quantité de mouvement

Soit une particule de masse m se déplaçant à la vitesse V. La quantité de mouvement de cette particule, en kg.m/s, se calcule avec la relation ci-dessous.

Q = m . V

Torseur cinétique

Le torseur cinétique est le torseur des quantités de mouvement d'un solide par rapport à un référentiel donné. Il comporte la résultante cinétique Rc et le moment cinétique Mc.

Résultante cinétique

Rc = m . V_G

m : Masse de solide, en kg.
V_G : Vitesse du centre d'inertie G du solide, en m/s.

Moment cinétique

Le moment cinétique se calcule simplement dans deux cas particuliers. Lorsque l'opérateur d'inertie est calculé au centre d'inertie G du solide ou lorsqu'il est calculé en un point fixe O.

Si l'opérateur d'inertie est calculé au centre d'inertie G :

Mc_G = J_G . Ω

Si l'opérateur d'inertie est calculé en un point fixe O :

Mc_O = J_O . Ω

Ω : Vecteur vitesse de rotation, en rad/s.

Energie cinétique

L'énergie cinétique d'un solide en mouvement est égale à la moitié du comoment du torseur cinétique par le torseur cinématique.

Ec = 12 {C}⊗{V}

Dans le cas où les deux torseurs sont écrits au centre d'inertie G :

Ec = 12 . Gm . V_G
J_G . Ω ⊗ GΩ
V_G = 12 . m . V_G ² + 12 . J_G . Ω ²