- Le travail de la force est positif.
- Le système 2 reçoit de énergie, le système 1 cède cette énergie.

- Le travail de la force est négatif.
- Le système 2 perd de l'énergie, le système 1 reçoit cette énergie.

L’énergie est une notion abstraite. Elle ne se touche pas, ne se voit pas, mais laisse percevoir ses effets : Elle change la position, la forme, la température, l'état (solide, liquide...) ou la composition chimique. L’énergie est une grandeur physique qui quantifie l'évolution d'un système matériel. L'énergie s'exprime normalement en joules (J), mais également en de nombreuses unités :
Prenons l'exemple de deux conducteurs reliant une lampe à une pile.

D'une manière générale, l'énergie peut être échangée, transformée ou stockée. Le rendement est le rapport entre l'énergie absorbée par un système et l'énergie utile fournie par ce système. Toujours compris entre 0 et 1, il s'exprime aussi sous la forme d'un pourcentage.
De manière imagée, le travail est la santé, l'énergie le repas équilibré nécessaire au maintien en bonne santé. Le travail est l'effort accompagnant le mouvement, l'énergie le carburant permettant à une machine de travailler... à notre place. Pour être plus précis, le repas équilibré et le carburant contiennent de l'énergie.
Lorsqu'un système (un gaz sous pression) exerce une action mécanique sur un autre système (le piston d'un moteur) en le déplaçant, il communique son énergie à ce système. Cette énergie est égale au travail de l'action mécanique.
Prenons le cas d'une force [vec]A1/2[/vec] exercée en A par un système 1 sur un système 2. Les deux systèmes étant en mouvement, le point d'application A de la force se déplace.


Le flux d'énergie s'exprime en terme de puissance : La puissance est l’énergie échangée par unité de temps. Elle s’exprime en watts (W).
P = [div]E[sur]t[/div]
P : Puissance, en W.
E : Energie échangée, en J.
t : Temps pendant lequel l'énergie est échangée, en s.
Remarque : Pour une raison historique, la puissance s'exprime aussi en cheval-vapeur.
1 ch = 735,5 W
Lorsqu'un système exerce une force sur un autre système en le translatant, il communique son énergie à ce système. Cette énergie est égale au travail de la force. Soit une force [vec]F[/vec] agissant sur un solide en translation rectiligne. Le solide se déplace de la distance MM'. La force est de direction, de sens et de norme constantes.

Le travail de la force est le produit de cette force par le déplacement de son point d'application :
W = [vec]F[/vec] . [vec]MM'[/vec] =
F . MM' . cos α
avec α = ([ang][vec]F[/vec], [vec]MM'[/vec][/ang])
W : Travail de la force, en J.
F : Force, en N.
MM' : Déplacement, en m.
Propriétés :
Remarques :
Lorsqu'un système exerce un couple sur un autre système en le faisant tourner, il communique son énergie à ce système. Cette énergie est égale au travail du couple. Soit un couple [vec]C[/vec] agissant sur un solide en rotation autour d'un axe fixe. Le solide tourne de l'angle θ. La direction du couple est celle de l'axe de rotation, son sens et sa norme restent constantes.

Le travail du couple est le produit de ce couple par le déplacement angulaire :
W = C . θ
W : Travail du couple, en J.
C : Couple, en N.m.
θ : Déplacement angulaire, en rad.
Soit une force [vec]F[/vec] agissant sur un solide en translation rectiligne.

La puissance de la force est le produit de cette force par la vitesse du solide :
P = [div][vec]F[/vec] . [vec]MM'[/vec][sur]t[/div] = [vec]F[/vec] . [div][vec]MM'[/vec][sur]t[/div] ⇒
P = [vec]F[/vec] . [vec]V[/vec] = F . V . cos α
F : Force, en N.Soit un couple [vec]C[/vec] agissant sur un solide en rotation autour d'un axe fixe. La direction du couple est celle de l'axe de rotation.

La puissance du couple est le produit de ce couple par la vitesse angulaire du solide :
P = [div]C . θ[sur]t[/div] ⇒
P = C . ω
C : Couple, en N.m.
ω : Vitesse angulaire du solide, en rad/s.
L'énergie hydraulique est, par exemple, l'énergie communiquée par un liquide à une machine hydraulique (pompe, turbine...). La formule ci-dessous s'applique pour des vitesses d'entrée et de sortie du fluide identiques.
P = Qv . ΔP
P : Puissance hydraulique, en W.
Qv : Débit volumique, en m3/s.
ΔP : Différence de pression entre les orifices d'entrée et de sortie de la machine hydraulique, en Pa.
Un diagramme des flux d'énergie, ou diagramme énergétique, est constitué :
Prenons l'exemple d'un générateur de courant alimentant un moteur électrique, lequel entraîne une machine. Le schéma ci-dessous représente le diagramme des flux d’énergie :

Une chaîne d'énergie se représente aussi sous forme fonctionnelle, avec des rectangles à l'intérieur desquels sont indiqués les fonctions des constituants.

Le vérin hydraulique transforme l'énergie hydraulique en énergie mécanique. Une partie de l’énergie reçue est cependant perdue à cause des frottements.

Energie hydraulique absorbée = Energie mécanique utile + Energie perdue.
Le système vis-écrou transforme l'énergie mécanique en une autre forme d'énergie mécanique. Une partie de l’énergie reçue est cependant perdue à cause des frottements.

Energie mécanique absorbée = Energie mécanique utile + Energie perdue.
L'alternateur transforme l'énergie mécanique en énergie électrique. Une partie de l’énergie reçue est cependant perdue à cause des frottements ou par effet Joule.
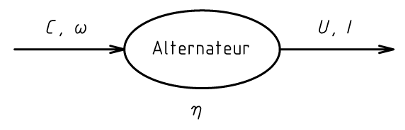
Energie mécanique absorbée = Energie électrique utile + Energie perdue.
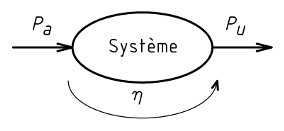
Un système qui transforme l'énergie absorbe une puissance et fournit une puissance utile. Le rendement du système est le rapport entre les puissances utile et absorbée :
η = [div]Pu[sur]Pa[/div]
η : Rendement.
Pu : Puissance utile, en W.
Pa : Puissance absorbée, en W.
Compte tenu des pertes, la puissance utile est toujours inférieure à la puissance absorbée. Ainsi, le rendement d'un système est toujours inférieur à 1.
Le rendement global de systèmes placés en série est le produit des rendements de chaque système :
η = η1 × η2 ×...× ηn
η1 : Rendement du système 1.
η2 : Rendement du système 2.
ηn : Rendement du système n.
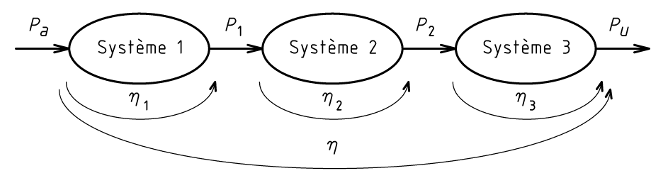
η = [div]Pu[sur]Pa[/div] = [div]Pu[sur]P2[/div] . [div]P2[sur]P1[/div] . [div]P1[sur]Pa[/div] = η1 . η2 . η3
Un système placé en altitude possède de l'énergie potentielle de gravité (ou de pesanteur). L’énergie potentielle de gravité de ce système varie en passant d'une altitude à une autre.
Ep2 - Ep1 = m . g . (z2 - z1)
Ep2 - Ep1 : Variation d’énergie potentielle de gravité, en J.
m : Masse du système, en kg.
g : Accélération de la pesanteur, en m/s2
z2, z1 : Altitudes, en m.
Plus simplement, on écrit : Ep = m . g . z
Remarque : La variation d'énergie potentielle de pesanteur est égale à l'opposé du travail du poids.
Un ressort soumis à de la compression ou à de la traction possède de l'énergie potentielle élastique. L’énergie potentielle élastique du ressort varie en passant d'une longueur à une autre.
Ep2 - Ep1 = [div]k[sur]2[/div] . (l0 - l2)2 - [div]k[sur]2[/div] . (l0 - l1)2
Ep2 - Ep1 : Variation d’énergie potentielle élastique, en J.
k : Raideur du ressort, en N/m.
l2, l1 : Longueurs du ressort sous charge, en m.
l0 : Longueur du ressort à vide, en m.
Plus simplement, on écrit : Ep = [div]k[sur]2[/div] . (l0 - l)2
Un gaz comprimé possède de l'énergie potentielle de pression. Le calcul de cette énergie est assez complexe car elle dépend du type de transformation.
Un solide en mouvement de translation rectiligne possède de l'énergie cinétique. L’énergie cinétique de ce solide varie en passant d'une vitesse à une autre.
Ec2 - Ec1 = [div]1[sur]2[/div] . m . (V22 - V12)
Ec2 - Ec1 : Variation d’énergie cinétique, en J.
m : Masse du solide, en kg.
V2, V1 : Vitesses, en m/s.
Plus simplement, on écrit : Ec = [div]1[sur]2[/div] . m . V 2
Un solide en mouvement de rotation autour d'un axe fixe (volant d"inertie) possède de l'énergie cinétique. L’énergie cinétique de ce solide varie en passant d'une vitesse angulaire à une autre.
Ec2 - Ec1 = [div]1[sur]2[/div] . J . (ω22 - ω12)
Ec2 - Ec1 : Variation d’énergie cinétique, en J.
J : Moment d'inertie du solide par rapport à l'axe de rotation, en kg.m2.
ω2, ω1 : Vitesses angulaires, en rad/s.
Plus simplement, on écrit : Ec = [div]1[sur]2[/div] . J . ω 2
Dans un repère galiléen, la variation d'énergie cinétique d'un solide S entre les instants t1 et t2 est égale à la somme algébrique des travaux de toutes les actions mécaniques extérieures appliquées à ce solide, entre les deux instants considérés.
Ec2 - Ec1 = W [alg]S[/alg]→S = [som][/som] Wact. ext./syst.
Les frottements de l'air étant négligés, une bille qui tombe n'est soumise qu'à son poids. L'augmentation de son énergie cinétique est due au travail du poids.
L’énergie mécanique totale que possède un système matériel est la somme algébrique de ses énergies potentielles et de son énergie cinétique. Si un système matériel est isolé, c'est à dire s'il n'échange aucune énergie avec son environnement, alors son énergie mécanique totale reste constante au cours du temps.
Em = Ec + ( Eppes. + Epelast. +Eppres. )
Em = constante
Contrairement au théorème de l'énergie cinétique :
Les frottements de l'air étant négligés, une bille qui tombe est un système matériel isolé dont l'énergie mécanique reste constante. L'augmentation de son énergie cinétique est due à la perte de son énergie potentielle.
Le stockage de l'énergie consiste à mettre en réserve de l'énergie pour l'utiliser ultérieurement. L'efficacité (ou rendement) du système est le rapport entre les énergies restituée et stockée :
η = [div]Er[sur]Es[/div]
η : Efficacité énergétique.
Er : Energie restituée, en J.
Es : Energie stockée, en J.
Compte tenu des pertes, l'énergie restituée est toujours inférieure à l"énergie stockée. Ainsi, l'efficacité d'un système de stockage est toujours inférieur à 1.
Caractéristiques d'un système de stockage :
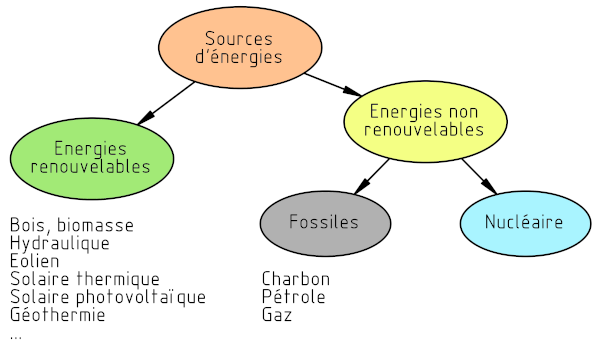
L'énergie peut être chimique, calorifique, nucléaire, solaire... Elle apparaît sous de nombreuses formes. Les produits que nous consommons sont fabriqués par des machines, alimentées essentiellement en électricité ou en combustible.
Les premières sources d'énergie utilisées par l'humanité étaient renouvelables. Puis elle s'est tournée vers des énergies épuisables, dont l'abondance a permis l'essor du monde moderne. Il lui faudra, dans l'avenir, revenir aux sources d'énergie renouvelables, avec une gestion durable de celles-ci.
L'énergie électrique est, par exemple, l'énergie communiquée par un courant électrique à un système électrotechnique ou électronique. Pour un courant continu :
P = U . I
P : Puissance instantanée du courant électrique, en W.
U : Tension du courant électrique aux bornes du système, en V.
I : Intensité du courant électrique, en A.
Trois sortes de courants électriques sont couramment utilisés :
Un combustible fournit de l'énergie thermique, suite à une réaction chimique. Les transformations de l'énergie qui font intervenir l'énergie thermique sont étudiées par la thermodynamique. Elles reposent sur un ensemble de lois dont deux sont de portée très générale : On les appelle des principes.