MECANIQUE DES FLUIDES

Introduction

Un fluide est un corps dont les forces de cohésion, entre les particules, sont très faibles. Il prend, par conséquent, la forme du récipient qui le contient.

Un fluide parfait est un fluide théorique et idéal, dans lequel les forces de cohésion sont nulles. Un tel fluide, s’il existait, s’étalerait en une pellicule infiniment mince si on le déposait sur une surface plane horizontale.

Propriétés des milieux fluides

Soit, dans un fluide, une facette plane, de surface élémentaire dS (très petite), séparant le fluide en deux zones 1 et 2. L’action de la zone 1 sur la zone 2, au niveau de la facette, est une force élémentaire représentée par le vecteur dF. Ce vecteur se décompose en deux composantes, l’une normale et l’autre tangentielle, notées respectivement dN et dT.

Contrainte normale

La contrainte normale σ se définit par la relation :

σ = p = dNdS

La contrainte normale représente la pression p (en N/mm² ou Mpa) au voisinage de la facette. Cette pression est indépendante de l’orientation de la facette.

Pressions relative et absolue

La pression peut être :

• Relative : Par rapport à la pression atmosphérique.
• Absolue : Dans ce cas, la pression du vide est nulle et la pression atmosphérique environ égale à 1 bar.

Contrainte tangentielle

La contrainte tangentielle τ se définit par la relation :

τ = dTdS

La contrainte tangentielle représente l’opposition au glissement relatif des couches fluides en mouvement. Elle est due à la viscosité du fluide. Si le fluide est parfait ou au repos, alors τ = 0.

Fluide newtonien

Un fluide newtonien est un fluide dont la loi contrainte – vitesse de déformation est linéaire. La viscosité d'un fluide newtonien est indépendante des contraintes qui lui sont appliquées.

Viscosités dynamique et cinématique

On distingue la viscosité dynamique et la viscosité cinématique. Soit deux facettes élémentaires parallèles, dV la vitesse de glissement d'une facette par rapport à l'autre et dz la distance (très petite) entre ces deux facettes.

La viscosité dynamique η, en Pa.s, se définit avec la relation :

τ = η . dVdz

dVdz représente le gradient de vitesse.

La viscosité cinématique ν, en m²/s, se définit avec la relation :

ν = ηρ

ρ est la masse volumique du fluide en kg/m³.

Hydrostatique

Loi fondamentale de l’hydrostatique

Soit un fluide :

• Au repos.
• Placé dans le champ de pesanteur g.
• Incompressible, de masse volumique constante ρ.

Dans ce fluide, considérons une portion de fluide de forme parallélépipédique. Notons V le volume, h la hauteur et S la surface de la face supérieure (ou inférieure) de ce parallélépipède. La portion de fluide, en équilibre, est soumises :

• A six actions de contact, sur chaque face du parallélépipède, dues à la pression du fluide environnant, notées F₁ à F₆.
• A une action à distance, le poids de la portion de fluide isolée, notée P.

D'après le Principe fondamental de la statique :

F₁ + F₂ + F₃ + F₄ + F₅ + F₆ + P = 0

Compte tenu de la symétrie du système :

F₃ = - F₄    et    F₅ = - F₆

Ce qui donne :

F₁ + F₂ + P = 0

Le calcul des normes de ces trois forces donne :

P = m . g = V . ρ . g = S . h . ρ . g
F₁ = p₁ . S
F₂ = p₂ . S

p₁ et p₂ sont les pressions au niveau des faces supérieures et inférieures du parallélépipède. La relation ci-dessous tient compte des sens des vecteurs représentant les forces.

S . h . ρ . g + p₁ . S - p₂ . S = 0 ⇒
h . ρ . g + p₁ - p₂ = 0 ⇒
p₁ - p₂ = - ρ . g . h

h est l'altitude entre deux particules fluides, l'une située sur la face supérieure et l'autre située sur la face inférieure. On note A et B ces particules fluides.

p_A - p_B = - ρ . g . (z_A - z_B)

D'une manière générale, la relation fondamentale de l'hydrostatique s'écrit :

p + ρ . g . z = Constante

p : Pression au voisinage de la particule en Pa.
ρ : Masse volumique du fluide en kg/m³.
g : Accélération de la pesanteur en m/s².
z : Altitude de la particule en m.

Théorème de Pascal

Supposons que les points A et B subissent les variations de pression Δp_A et Δp_B. D’après la loi fondamentale de l’hydrostatique :

(p_A + Δp_A) - (p_B + Δp_B) = - ρ . g . (z_A - z_B) ⇒
Δp_A - Δp_B = - p_A + p_B - ρ . g . (z_A - z_B) ⇒
Δp_A = Δp_B

Le théorème de Pascal s'énonce ainsi : Dans un fluide incompressible en équilibre, toute variation de pression en un point entraîne la même variation de pression en tout point.

Théorème d’Archimède

Si on reprend le parallélépipède fluide précédent, la résultante F des forces exercées par le fluide sur le parallélépipède est égal à :

F = F₁ + F₂ + F₃ + F₄ + F₅ + F₆

D'après le Principe fondamental de la statique :

F + P = 0 ⇒
F = P = poids du fluide

Si le parallélépipède fluide est remplacé par un parallélépipède dans un matériau quelconque, alors le poids du fluide de la relation ci-dessus est remplacé par le poids du parallélépipède qui serait constitué du fluide environnant, autrement dit le poids du fluide déplacé.

Le théorème d’Archimède s'énonce ainsi : L’action d’un fluide en équilibre sur un solide immergé a pour résultante une force verticale, dirigée vers le haut, de norme le poids du fluide déplacé, de point d’application le centre de gravité du fluide déplacé. Cette force est appelée poussée d’Archimède.

Action d'un fluide sur une paroi verticale

Norme de la résultante des forces de pression :

R = h₀p(z) . l . dz    ⇒    R = l . h . p₀ + ρ . g . h2

Centre de poussée :

d . R = h₀z . p(z) . l . dz    ⇒    d = h2 . p₀ + ρ . g . h3 p₀ + ρ . g . h2

Remarques

• ρ . g . h est négligeable devant p₀ dans le cas d’un gaz agissant sur le piston d’un vérin.
• p₀ est négligeable devant ρ . g . h dans le cas d’un barrage hydraulique.

Dynamique des fluides

Description d'un écoulement

Types d'écoulement

Un écoulement dans une conduite est laminaire si les trajectoires des particules sont des lignes régulières.

L'écoulement est turbulent si les trajectoires des particules s’entrevêchent, s’enroulent sur elles-mêmes.

La distribution des vitesses, dans le cas de l’écoulement laminaire d’un fluide réel ou visqueux dans une conduite, montre que les particules fluides n’ont pas toutes la même vitesse.

Débit volumique

Le débit volumique se calcule avec la relation :

Q_v = V_moy . S

Q_v : Débit volumique en m³/s.
V_moy : Vitesse moyenne du fluide en m/s.
S : Section de passage en m².

Débit massique

Le débit massique se calcule avec la relation :

Q_m = ρ . Q_v

Q_m : Débit massique en kg/s.
ρ : Masse volumique du fluide en kg/m³.

Equation de continuité

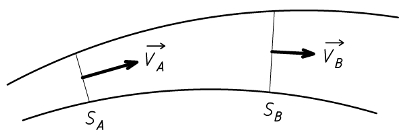
Dans une conduite exempte de fuite, la quantité de fluide entrant est égale à la quantité de fluide sortant. L'équation de continuité peut s'écrire sous plusieurs formes. Pour un fluide incompressible, le débit volumique reste constant au cours du temps.

Q_{V A} = Q_{V B}    ⇒    V_A . S_A = V_B . S_B

Nombre de Reynolds

Ce nombre sans dimension permet de prévoir le type d'écoulement dans une conduite. Il se calcule en fonction d'une dimension caractéristique de l'écoulement. Pour une conduite cylindrique, il s'agit du diamètre.

Re = V_moy . dν

V_moy : Vitesse moyenne du fluide en m/s.
d : Diamètre de la conduite en m.
ν : Viscosité cinématique en m²/s.

• Re < 2300 : L'écoulement est laminaire.
• Re > 3000 : L'écoulement est turbulent.
• 2300 < Re < 3000 : L'écoulement fluctue entre le régime laminaire et le régime turbulent.

Pertes de charges régulières et singulières

Considérons un liquide circulant dans une conduite horizontale de section constante. Deux tubes plongent dans le liquide en A et B, le liquide s'écoulant de A vers B. Du fait des frottements à l’intérieur de la conduite, le liquide perd de son énergie au fil de l'écoulement, de sorte que le niveau en D soit inférieur au niveau en C. On appelle perte de charge cette dissipation d'énergie.

Les paramètres suivants font augmenter la perte de charge :

• La conduite est longue, de faible section.
• La conduite comporte de nombreux coudes, des variations brusques de section.
• Le fluide est visqueux.
• Le débit est important.
• Le type d'écoulement, laminaire ou turbulent, joue également un rôle important.

On distingue :

• Les pertes de charges régulières ou linéaires, qui interviennent dans une conduite rectiligne de section constante, généralement proportionnelles à la longueur de la conduite.
• Les pertes de charges singulières, dues aux accidents de canalisation : Coudes, changement de section, appareils de mesures...

La perte de charge s'exprime en diverses unités :

• On l'exprime en hauteur de fluide. Lorsque l'eau est pris comme fluide de référence, on l'exprime en mce (mètres de colonne d'eau).
• S'agissant d'une diminution de pression entre l'amont et l'aval, on l'exprime également en Pa.
• Puisqu'elle correspond à une perte d'énergie, on l'exprime aussi en J/kg.

Loi de Poiseuille

Cette loi introduit la notion de résistance hydraulique d'une conduite, dans laquelle circule un fluide en régime laminaire. La résistance hydraulique est proportionnelle à la longueur de la conduire. On écrit :

J_AB = R . Q_v

J_AB : Perte de charge, en Pa.
R : Résistance hydraulique, en Pa.s/m³.
Q_v : Débit volumique, en m³/s.

Si on compare la loi de Poiseuille à la loi d'Ohm :

• La perte de charge en Pa correspond à la tension en V.
• Le débit volumique en m³/s correspond à l'intensité en A.

Théorème de Bernoulli

L'équation de Bernoulli s'applique si :

• L'écoulement du fluide est permanent.
• Le fluide est incompressible (sa masse volumique reste constante).

Cas d’un écoulement sans échange de travail

Pour un fluide parfait, on montre, à partir du principe de conservation de l’énergie, la relation de Bernoulli :

V ²2 + pρ + g . z = Cte

V : Vitesse d'une particule fluide en m/s.
p : Pression au voisinage de la particule en Pa (1 bar = 1 daN/cm² = 10⁵ Pa = 0,1 N/mm²).
ρ : Masse volumique du fluide en kg/m³.
g : Accélération de la pesanteur en m/s².
z : Altitude de la particule en m.

Pour deux particules fluides A et B, la relation de Bernoulli devient :

12 ( V_B ² - V_A ² ) + 1ρ . ( p_B - p_A ) + g . ( z_B - z_A ) = 0

Pour un fluide réel, il faut prendre en compte des pertes de charge J_AB, exprimées en J/kg. L'écoulement s'effectuant de A vers B, la valeur de J_AB est négative. La relation de Bernoulli devient :

12 ( V_B ² - V_A ² ) + 1ρ . ( p_B - p_A ) + g . ( z_B - z_A ) = J_AB

La relation de Bernoulli s'écrit sous deux autres formes. Dans la deuxième forme ci-dessous, chaque terme de la relation représente une hauteur, en m.

12 . g ( V_B ² - V_A ² ) + 1ρ . g . ( p_B - p_A ) + ( z_B - z_A ) = J_AB

Dans cette troisième forme, chaque terme de la relation représente une pression, en Pa.

ρ2 ( V_B ² - V_A ² ) + ( p_B - p_A ) + ρ . g . ( z_B - z_A ) = J_AB

Cas d’un écoulement avec échange de travail

Si le fluide traverse une machine hydraulique, alors il échange de l’énergie E avec cette machine :

• E > 0 si la machine fournit de l’énergie au fluide (cas d’une pompe).
• E < 0 si le fluide fournit de l’énergie à la machine (cas d’une turbine).

L’équation de Bernoulli devient alors :

12 ( V_B ² - V_A ² ) + 1ρ . ( p_B - p_A ) + g . ( z_B - z_A ) = E + J_AB

L’énergie E s’exprime ici en J/kg. La puissance P en W de la machine hydraulique se calcule avec la relation :

P = E . Q_m

Q_m est le débit massique en kg/s.

Comparaison entre une machine hydraulique et une machine électrique

Souvent, dans une machine hydraulique :

• La différence d'altitude z_B - z_A est négligeable.
• Les sections d'entrée et de sortie sont identiques de sorte que V_B = V_A.
• Les pertes de charge n'ont pas réellement de sens, la machine hydraulique ayant un rendement.

En conséquence, l'équation de Bernoulli se simplifie. La puissance hydraulique se calcule alors avec la relation :

P = E . Q_m = 1ρ . ( p_B - p_A ) . Q_m = ( p_B - p_A ) . Q_mρ ⇒

P = Δp . Q_v

Si on compare la machine hydraulique à la machine électrique :

• La différence de pression en Pa correspond à la tension en V.
• Le débit volumique en m³/s correspond à l'intensité en A.

Rendement d’un système hydraulique

Le rendement η d’une machine hydraulique est le rapport entre la puissance qu’elle reçoit et la puissance qu’elle fournie. Soit P_a la puissance sur l’arbre et P_f la puissance échangée avec le fluide.

η = P_fP_a    pour une pompe et   η = P_aP_f    pour une turbine.

Théorème d'Euler

Enoncé

Considérons une portion de fluide incompressible circulant dans une conduite.

Cette portion de fluide est délimitée par :

• La surface d'entrée S_A, traversée par le fluide.
• La surface de sortie S_B, également traversée par le fluide.
• La surface latérale S_L.

Cette portion de fluide est soumise à plusieurs actions mécaniques :

• Son poids P .
• La force F_A due à la pression p_A du fluide agissant sur la surface S_A.
• La force F_B due à la pression p_B du fluide agissant sur la surface S_B.
• La force F_L exercée par la surface S_L.

Le fluide étant en mouvement, la somme des forces extérieures ne donne pas le vecteur nul. On se place dans le cas d'un régime stationnaire. Le théorème d'Euler est vrai également dans le cas d'un fluide visqueux.

Q_m ( V_B - V_A ) = F ext.  ⇒
Q_m ( V_B - V_A ) = P + F_A + F_B + F_L

Q_m : Débit massique, en kg/m³.
V_A : Vitesse moyenne d'entrée du fluide, en m/s.
V_B : Vitesse moyenne de sortie du fluide, en m/s.
F ext. : Somme des forces extérieures, en N.

Application : Action d'un jet d'eau sur une paroi

Soit un jet d'eau suffisamment puissant pour être considéré horizontal, projeté sur une paroi verticale de surface S. L'eau poussant la paroi, cette dernière est retenue par la force F. L'ensemble est situé dans de l'air à la pression atmosphérique Pa.

Appliquons le théorème d'Euler et projetons sur x:

- Q_m . V_A = - F_paroi/eau + Pa.S

Les forces F_paroi/eau et F_eau/paroi étant égales en norme :

- Q_m . V_A = - F_eau/paroi + Pa.S

On isole maintenant la paroi, en équilibre :

F_eau/paroi - Pa.S - F = 0  ⇒ F_paroi/eau + Pa.S = - F

On en déduit :

F = Q_m . V_A

Remarque

Si la paroi paroi se déplace à la vitesse V_paroi alors :

F = Q_m . ( V_A - V_paroi )

Point de fonctionnement d'un circuit hydraulique

Considérons une pompe déplaçant un fluide dans un circuit hydraulique :

• Plus le débit souhaité est important, plus la pompe doit fournir une pression élevée.
• En général, la pression que peut délivrer une pompe diminue lorsque le débit augmente.

Il est donc possible de tracer deux courbes sur un même graphique, pour obtenir le point de fonctionnement.