





La mécanique est la science des mouvements, des équilibres, des forces et des énergies qu'ils mobilisent.
Modéliser signifie transformer un problème réel en problème mathématique. Généralement, il existe plusieurs modèles possibles pour un même problème réel. Certains modèles ont l'avantage d'être simples. D'autres représentent plus fidèlement la réalité.
Une liaison théorique et idéale est constituée de pièces indéformables, aux surfaces géométriquement parfaites, sans jeu et sans frottement. En réalité, toutes les pièces sont déformables. Les surfaces sont rugueuses et les jeux indispensables au bon fonctionnement de la liaison. Les frottements s'opposent aux déplacements.
Une liaison fait intervenir un ensemble de pièces solides. Il est donc nécessaire de définir la notion de solide :
C'est un solide théorique et idéal tel que, quels que soient A et B deux points de ce solide, la distance AB reste constante, au cours du temps pendant lequel se déroule son étude.

Concrètement, les pièces d'un mécanisme sont, pour la plupart, assimilées à des solides indéformables. La notion de temps pendant lequel se déroule l'étude a aussi son importance.
Un solide est souvent constitué de plusieurs pièces considérées indéformables, fixées entre elles à l’aide de vis, de clavettes, de goupilles... Ces pièces constituent un groupe cinématiquement lié. On dit aussi qu’elles appartiennent à une classe d’équivalence de l’ensemble des pièces du mécanisme, muni de la relation "sans mouvement relatif".
C'est un ensemble de solides liés entre eux par des liaisons. On parle de système car le mouvement d'un solide dépend des mouvements des solides environnants.
Le contact entre deux solides peut être ponctuel, linéique ou surfacique.
| Contacts ponctuels | Contacts linéiques | Contacts surfaciques |
|---|---|---|
Sphère sur plan |
Cylindre sur plan |
Plan sur plan |
Cylindre sur cylindre |
Sphère dans cylindre |
Cylindre dans cylindre |
Pour décrire les mouvements relatifs entre deux solides, on définit un repère local associé au contact.
On notera que le repère local associé au contact n’est lié à aucun des solides en présence. Par exemple, dans le cas d'une bille roulant sur une surface plane, le centre de liaison est le point de contact, lequel n'est lié ni à la bille, ni au plan.

La géométrie d’un contact ne suffit pas à caractériser une liaison.
Un contact cylindre dans cylindre engendre une liaison :


Considérons deux solides en contact. Un degré de liberté, c'est une possibilité de mouvement, de translation ou de rotation, selon un des trois axes du repère local associé au contact.
Un solide sans liaison aucune possède six degrés de liberté :
On appelle liaison tout obstacle qui supprime un ou plusieurs degrés de liberté entre deux solides. La nature d’une liaison ne dépend que des degrés de liberté entre les deux solides.
L'association deux à deux des surfaces géométriques élémentaires, que sont le plan, le cylindre et la sphère, permet d'introduire six liaisons dites simples ou élémentaires.
| Surfaces géométriques | Liaison |
|---|---|
| Plan-plan | Appui-plan |
| Cylindre-cylindre | Pivot-glissant |
| Sphère-sphère | Rotule |
| Cylindre-plan | Linéaire-rectiligne |
| Sphère-plan | Ponctuelle |
| Sphère-cylindre | Linéaire-annulaire |
On parle de liaison composée lorsque deux solides sont liés entre eux par plusieurs liaisons élémentaires. Dans l'exemple ci-dessous, la liaison entre les solides 1 et 2 est une liaison appui-plan, composée d'une liaison linéaire-rectiligne et d'une liaison ponctuelle.

Les liaisons composées ci-dessous ont été retenues car leur rôle en technologie de construction est important, en particulier pour les fonctions de guidage et de mise en position.
Les six liaisons élémentaires auxquelles s'ajoutent cinq liaisons composées constituent les liaisons normalisées.
| Nom de la liaison | Représentation spatiale | Représentation(s) dans le plan | Degré(s) de liberté |
|---|---|---|---|
| Encastrement en A |  |  |
Aucun degré de liberté |
| Pivot d'axe (Ax) |
 |  |
1 degré de liberté Rx |
| Glissière d'axe (Ax) |
 |  |
1 degré de liberté Tx |
| Hélicoïdale d'axe (Ax) |
 |  |
1 degré de liberté Tx et Rx conjuguées |
| Pivot-glissant d'axe (Ax) |
 |  |
2 degrés de liberté Tx et Rx |
| Rotule ou sphérique de centre A |
 |  |
3 degrés de liberté Rx, Ry et Rz |
| Sphérique à doigt de centre A bloquée en z |
 |  |
2 degrés de liberté Rx et Ry |
| Appui-plan de normale (Az) |
 |  |
3 degrés de liberté Tx, Ty et Rz |
| Linéaire-annulaire d'axe (Ax) |
 |  |
4 degrés de liberté Tx, Rx, Ry et Rz |
| Linéaire-rectiligne de normale (Az) de droite de contact (Ax) |
 | 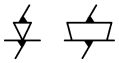 |
4 degrés de liberté Tx, Ty, Rx et Rz |
| Ponctuelle de normale (Az) |
 |  |
5 degrés de liberté Tx, Ty, Rx, Ry et Rz |
Le graphe des liaisons d'un mécanisme fait apparaître :
Graphe des liaisons :

Groupes cinématiquement liés :
Description des liaisons :
Un schéma cinématique représente :
Un schéma cinématique est dit minimal s'il ne fait intervenir que les groupes de pièces cinématiquement liées (classes d'équivalence). Il peut être dessiné en vue plane ou en perspective.

Elle concerne les symboles de base utilisés dans la définition de la mise en position géométrique d'une pièce. Elle ne permet pas de connaître les technologies utilisées pour la mise en position et pour le maintien en position.
| Symboles de base | |
|---|---|
 |  |
Exemple d'une liaison appui-plan :
| Symbolisations frontales équivalentes | Symbolisation projetée | |
|---|---|---|
| Représentation normale | Représentation simplifiée | |
 |  |  |
Elle concerne les symboles utilisés sur les contrats de phase pour représenter les éléments d'appui et de maintien des pièces au cours de l'usinage. Chaque symbole se construit à l'aide de quatre éléments.

Nature de la surface et fonction de l'élément technologique :
| Nature de la surface | Fonction de l'élément technologique | |
|---|---|---|
| MIP (mise en position) | MAP (maintien en position) | |
| Surface usinée |  |  |
| Surface brute |  |  |
Exemples du type de technologie et de la nature du contact :
| Symbole | Signification | |
|---|---|---|
 |
Touche plate fixe de départ d'usinage en appui sur une surface usinée | |
 |
Touche bombée fixe de départ d'usinage sur une surface brute | |
 |
Mors striés à serrage concentrique flottant utilisés comme entraîneurs sur une surface brute | |
 |
Touche bombée de soutien irréversible sur surface brute | |
Une table à trois pieds repose toujours sur ses trois pieds. Pouvant se translater horizontalement ou tourner autour d'un axe vertical, elle constitue une liaison appui-plan avec le sol. La liaison entre un pied de table et le sol étant ponctuelle, les trois liaisons ponctuelles forment une liaison appui-plan. Celle-ci est isostatique.
Une table à quatre pieds est bancale si la planéité du sol ou la souplesse de la table sont insuffisantes. La liaison appui-plan équivalente aux quatre liaisons ponctuelles est hyperstatique d'ordre 1. Si la table comportait cinq pieds, la liaison équivalente serait hyperstatique d'ordre 2.
Il est fréquent, en mécanique, que plusieurs liaisons soient équivalentes à une seule liaison. Lors de la conception d'une liaison, on cherche à ce que son degré d'hyperstatisme soit le plus faible possible.
Le montage sur deux roulements à billes est un exemple classique. Le roulement supportant la charge axiale est modélisé avec une liaison rotule, l'autre roulement avec une liaison linéaire-annulaire. Les deux liaisons forment une liaison pivot.



n liaisons L1, L2, ..., Ln sont en parallèle entre deux solides S0 et S1 si chaque liaison relie directement ces deux solides.

Au niveau de chaque liaison, une action mécanique est transmise par le solide S1 sur le solide S0. Notons {T1}, {T2}, ... , {Tn} les torseurs d'action mécanique correspondants.
Le torseur équivalent s'écrit : {Téq.} = {T1} + {T2} + ... + {Tn}
La forme du torseur équivalent permet de déduire la nature de la liaison équivalente.
Si on néglige le poids, le PFS appliqué au solide S0 s'écrit : {Téq.} = {0}. Il en résulte un système de rs équations indépendantes à Ns inconnues.
A partir de rs et de Ns, on calcule :
Dans un montage d'usinage pour une pièce de forme prismatique, la mise en position est souvent réalisée avec six appuis fixes à contact ponctuel, notés 1 à 6. Chaque appui est une liaison ponctuelle supprimant un degré de liberté.

n liaisons L1, L2, ..., Ln sont en série entre deux solides S0 et Sn si elles sont disposées à la suite l'une de l'autre par l'intermédiaire de (n-1) solides.

Au niveau de chaque liaison Li, une action mécanique est transmise par le solide Si sur le solide Si-1. Notons {Ti} le torseur d'action mécanique correspondant.
Si on néglige les poids, le PFS appliqué sur chaque solide s'écrit : {T1} = {T2}, {T2} = {T3}, ... , {Tn-1} = {Tn}
Le torseur équivalent s'écrit : {Téq.} = {T1} = {T2} = ... = {Tn}
La forme du torseur équivalent permet de déduire la nature de la liaison équivalente.
La liaison rotule entre les pièces 2 et 4 et la liaison appui-plan entre les pièces 4 et 7 forment une liaison ponctuelle entre les pièces 2 et 7. L'intérêt de ce pied à rotule est de remplacer un contact ponctuel par un contact surfacique. Celui-ci supporte des efforts bien plus importants qu'un contact ponctuel.
