| Sollicitation | Résistance | Déformation |
|---|---|---|
| Traction-compression |
σ = [div]F[sur]So[/div] Rpe = [div]Re[sur]s[/div] σ ≤ Rpe |
σ = E.ε ε = [div]ΔL[sur]Lo[/div] |
| Cisaillement |
τ = [div]F[sur]S[/div] Rpg = [div]Reg[sur]s[/div] Reg ≈ [div]Re[sur]2[/div] τ ≤ Rpg |
- |
| Flexion |
σ = [div]Mf[sur]IGz[/div] . v Rpe = [div]Re[sur]s[/div] σ ≤ Rpe |
y" = [div]Mf[sur]E.IGz[/div] |
| Torsion |
τ = [div]Mt[sur]IGx[/div] . v Rpg = [div]Reg[sur]s[/div] Reg ≈ [div]Re[sur]2[/div] τ ≤ Rpg |
α = θ.L θ = [div]Mt[sur]G.IGx[/div] |
| Sollicitations composées |
Tresca : σe = [rac]σ 2 + 4.τ 2[/rac] Von Mises : σe = [rac]σ 2 + 3.τ 2[/rac] |
Principe de superposition |
L'exemple de programme en Python ci-dessous produit la déformée d'une poutre posée sur deux appuis et chargée en son centre.
import matplotlib.pyplot as plt
import numpy as np
P = 200 # Force exercée sur la poutre (N)
L = 500 # Longueur de la poutre (mm)
E = 200000 # Module d'Young (MPa)
I = 70000 # Moment quadradratique (mm⁴)
x = np.linspace(0,L,200)
y = (x<=L/2)*P*(4*x**3-3*x*L**2)/(48*E*I) + (x>L/2)*P*(4*(L-x)**3-3*(L-x)*L**2)/(48*E*I)
plt.figure("Poutre en flexion sur deux appuis")
plt.title("Flèche maximale : "+str(round(-1*np.min(y),3))+" mm")
plt.xlabel("Poutre (mm)")
plt.ylabel("Flèche (mm)")
plt.grid(True)
plt.plot(x, y, color='#ff0000')
plt.show()

Le module d’un engrenage se calcule classiquement avec la formule :
m = 2,34 . [rac][div]Ft[sur]k . Rpe[/div][/rac]
Avec Ft = F . cos(α) et k = [div]b[sur]m[/div]
m : Module, en mm
Ft : Force tangentielle, en N
k : Coefficient de largeur de denture
Rpe : Résistance pratique à l'extension du matériau, en MPa
F : Force sur une dent, en N
α : Angle de pression (20° pour une denture normalisée)
b : Largeur de denture, en mm
Une dent est assimilée à une poutre :

Les sollicitations de compression et de cisaillement sont négligées.
Mf = 2,25 . m . Ft
[div]IGz[sur]v[/div] = [div]b . (0,5 . π . m)2[sur]6[/div] = [div]k . π2 . m3[sur]24[/div]
σmax = Rpe = [div]Mf[sur]IGz[/div] . v = [div]2,25 . m . Ft . 24[sur]k . π2 . m3[/div] = [div]2,25 . Ft . 24[sur]k . π2 . m2[/div] = [div]5,47 . Ft[sur]k . m2[/div]
m2 = [div]5,47 . Ft[sur]k . Rpe[/div]
m = [rac][div]5,47 . Ft[sur]k . Rpe[/div][/rac] = 2,34 . [rac][div]Ft[sur]k . Rpe[/div][/rac]
La raideur d’un ressort se calcule communément avec la formule :
k = [div]G . d 4[sur]8 . D 3 . n[/div]
k : Raideur du ressort, en N/mm
G : Module d’élasticité transversal du matériau, en MPa
d : Diamètre du fil, en mm
D : Diamètre moyen du ressort, en mm
n : Nombre de spires utiles du ressort
Une étude approfondie montrerait que le fil constituant le ressort agit essentiellement en torsion. Les autres sollicitations sont négligeables. Considérons un ressort :
L'approche énergétique facilite la résolution du problème. De manière simplifiée :
W = F . x = Mt . α
F . x = Mt . θ . L
Pour une spire complète : L = π . D
F . x = Mt . [div]Mt[sur]G . IGx[/div] . π . D = Mt2 . [div]π . D[sur]G . IGx[/div]
Isoler un quart de spire mène à l'égalité :
Mt = F . [div]D[sur]2[/div]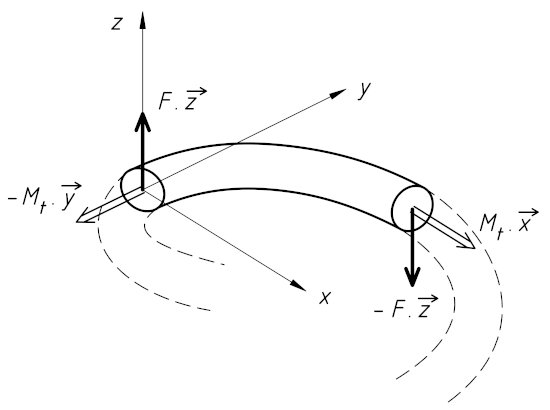
F . x = F2 . [div]D2 . π . D[sur]4 . G . IGx[/div]
x = F . [div]D3 . π[sur]4 . G . IGx[/div]
k = [div]F[sur]x[/div] = [div]4 . G . IGx[sur]D3 . π[/div] = [div]4 . G . π . d4[sur]D3 . π . 32[/div] = [div]G . d4[sur]8 . D3[/div]
Cette raideur k correspond à une seule spire. Pour n spires, la longueur L est multipliée par n. On retrouve ainsi la formule de départ.