Le calcul des contraintes dans une poutre permet de savoir si elle résistera ou pas. Un coefficient de sécurité est choisi pour limiter le risque de détérioration.
Une sollicitation est dite simple si l'action mécanique s'exerçant au sein d'une section droite de la poutre a pour résultante un effort normal, un effort tranchant, un moment de torsion ou un moment de flexion. Il existe donc quatre sollicitations simples :
Les autres sollicitations sont dites composées. La flexion-torsion et la flexion-traction en sont deux exemples. Si on ajoute aux quatre sollicitations simples la flexion simple (qui est une sollicitation composée), on obtient les cinq sollicitations élémentaires, relatives aux cas de charges couramment rencontrés.
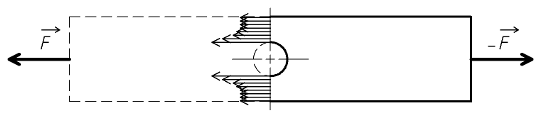
Si on tire sur les extrémités d'une poutre, elle est soumise à de la traction. Si on pousse sur ses extrémités de manière à la comprimer sans qu'il y ait de flambage, elle est soumise à de la compression.

La poutre étant coupée fictivement en deux parties, l'action du tronçon de droite sur le tronçon de gauche
a pour résultante l'effort normal

{ T coh. } =
G {
Tout point de la section de coupure est soumis à la même contrainte normale σ.
La contrainte normale σ se calcule avec la relation :
σ =
So : Section de coupure (poutre au repos), en mm2.
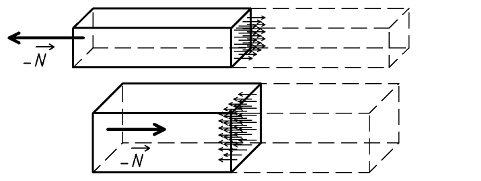
Si à droite d'une section donnée la poutre est soumise à une force transversale et à gauche de cette même section, à une force transversale opposée, elle est soumise à du cisaillement.
La poutre étant coupée fictivement en deux parties, l'action du tronçon de droite sur le tronçon de gauche
a pour résultante l'effort tranchant
{ T coh. } =
G {
Tout point de la section de coupure est soumis à la même contrainte tangentielle τ.
La contrainte tangentielle τ se calcule avec la relation :
τ =
S : Section de coupure, en mm2.
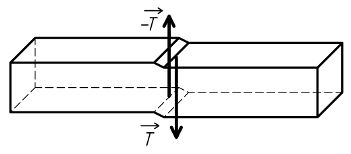
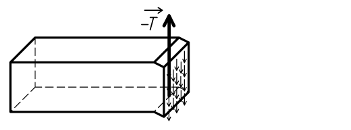
Si on exerce à l'extrémité d'une poutre un couple, et à l'autre extrémité un autre couple de sens opposé, ces couples ayant pour direction celle de la ligne moyenne, elle est soumise à de la torsion.
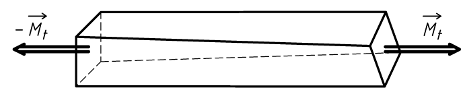
La poutre étant coupée fictivement en deux parties, l'action du tronçon de droite sur le tronçon de gauche
a pour résultante le moment de torsion
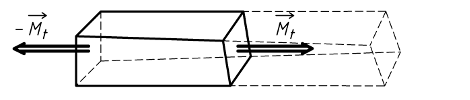
{ T coh. } =
G {
Tout point de la section de coupure est soumis à une contrainte tangentielle τ. Plus ce point est éloigné du barycentre G, plus cette contrainte est importante. La contrainte est proportionnelle à l'éloignement.
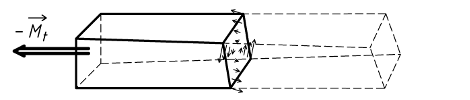
La contrainte tangentielle maximale τmax se calcule avec la relation :
τmax =
IGx : Moment quadratique de la section de coupure par rapport à l'axe (Gx), en mm4.
v : Distance maximale entre un point de la section de coupure et le point G, en mm.
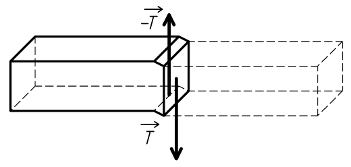
Si on exerce à l'extrémité d'une poutre un couple, et à l'autre extrémité un autre couple de sens opposé, ces couples ayant une direction perpendiculaire à celle de la ligne moyenne, elle est soumise à de la flexion pure.
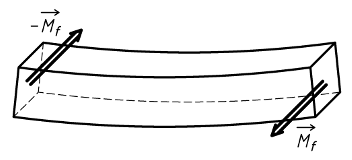
La poutre étant coupée fictivement en deux parties, l'action du tronçon de droite sur le tronçon de gauche
a pour résultante le moment de flexion
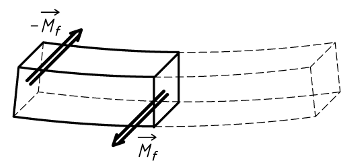
{ T coh. } =
G {
Tout point de la section de coupure est soumis à une contrainte normale σ. Plus ce point est éloigné de l'axe (Gz), plus cette contrainte est importante. La contrainte est proportionnelle à l'éloignement.
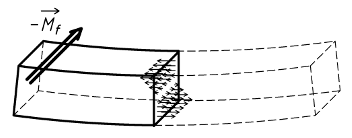
La contrainte normale maximale σmax se calcule avec la relation :
σmax =
IGz : Moment quadratique de la section de coupure par rapport à l'axe (Gz), en mm4.
v : Distance maximale entre un point de la section de coupure et l'axe (Gz), en mm.
On note généralement :
Selon le cas, la contrainte maximale dans la pièce doit être inférieure à une des limites ci-dessus.
La plupart des matériaux résistent aussi bien en traction qu'en compression.
On a alors : Re = Rec
D'autres matériaux, comme le béton, résistent mieux en compression qu'en traction.
On a alors : Re < Rec
Le rapport entre Re et Reg dépend du matériau.
Pour simplifier et par précaution, on retient souvent le facteur le plus défavorable.
On pose alors : Reg = 0,5 x Re
| Matériau | Reg/Re |
|---|---|
| Aciers doux, alliages d'aluminium | ≈ 0,5 |
| Aciers mi-durs | 0,7 |
| Aciers durs et fontes | ≈ 0,8 |
Pour des raisons de sécurité et d'incertitude sur les hypothèses, on définit le coefficient de sécurité s, toujours supérieur à 1 et sans unité. La contrainte maximale dans la pièce doit rester inférieure à la résistance pratique.
Rpe =
Rpc =
Rpg =
Le flambement ou flambage est un phénomène d'instabilité apparaissant lorsqu'une poutre à grand allongement est soumise à de la compression. La section de coupure est alors soumise à un effort normal, mais également à un moment de flexion. Pour une poutre de section constante, la charge critique de flambage théorique peut se calculer avec la formule d'Euler.
Fc =
Fc : Charge critique, en N.
E : Module d'Young, en MPa.
IGz : Moment quadratique par rapport à l'axe (Gz), en mm4.
L : Longueur de la poutre, en mm.
A partir des contraintes normale σ et tangentielle τ calculées en un point de la section de coupure, on détermine la contrainte normale équivalente σe. On recherche le point de la section de coupure pour lequel σe est maximal. La valeur maximale de σe est ensuite comparée à la résistance pratique à la traction Rpe.
Contrainte de Tresca :
σe =
Contrainte de Von Mises :
σe =
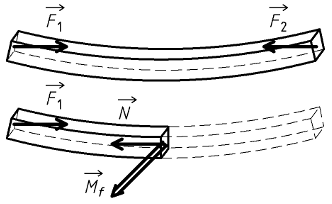
La flexion simple constitue un cas classique de sollicitations composées. Elle est plus courante que la flexion pure. Le torseur des efforts de cohésion comporte un moment de flexion et un effort tranchant.
{ T coh. } =
G {
L'exemple ci-dessous est celui d'une poutre chargée, posée sur deux appuis à ses extrémités.
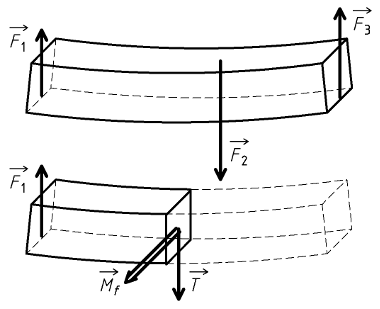
Les valeurs de T et de Mf varient en fonction de la section de coupure, dont la position est repérée par son abscisse x. Les diagrammes des efforts tranchants et des moments de flexion permettent repérer rapidement les parties les plus sollicitées de la poutre. Ci-dessous, ces diagrammes ont été tracés en isolant le tronçon de gauche.

Diagramme des efforts tranchants :
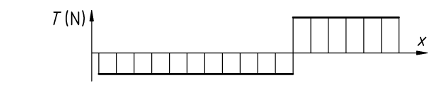
Diagramme des moments de flexion :

La concentration des contraintes est un problème souvent rencontré dans la conception mécanique. C’est un phénomène d’augmentation locale des contraintes dans une zone comportant une variation importante de section.
Dans l'exemple d'une plaque percée soumise à de la traction, la zone située à proximité du trou est la plus sollicitée. La contrainte réelle maximale σmax au voisinage du trou est le produit de la contrainte nominale (contrainte théorique sans concentration de contrainte) σnom par le coefficient de concentration de contraintes Kt.
σmax = σnom . Kt

La contrainte réelle maximale est comparée à la résistance pratique à la traction Rpe.
σmax ≤ Rpe
Le coefficient de concentration de contraintes se détermine de diverses manières :
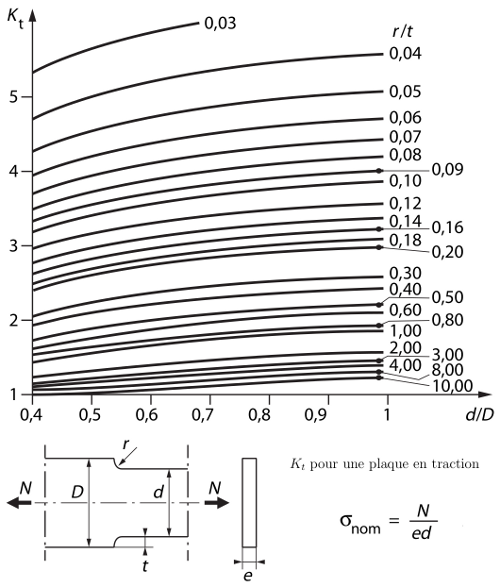
Les matériaux ductiles sont peu affectés par les concentrations des contraintes, contrairement aux matériaux durs.