
Toute pièce se déforme lorsqu'elle est soumise à des actions mécaniques. L'amplitude des déformations dépend des formes et du matériau constituant la pièce. Elle augmente avec l'intensité des actions exercées et peut conduire à la rupture. La résistance des matériaux (RDM) a pour objet :
La RDM propose différents outils :
Dans une étude de RdM, le matériau est généralement considéré :
La forme de solide usuelle est la poutre, c'est à dire un solide de forme allongée.
Pour être plus précis, une poutre est un solide engendré par le déplacement d'une surface plane S, dont le barycentre (ou centre de surface) G décrit une ligne Δ, perpendiculaire en tout point au plan contenant S. La ligne Δ est appelée ligne moyenne.

Les caractéristiques d'une poutre sont :
La pièce se déformant peu, l'influence des déformations sur les positions des points d'application des charges est négligeable.
Par exemple, dans le cas de la poutre ci-dessous chargée et encastrée à ses extrémités, si la déformation est petite, le moment en A est proportionnel à la longueur AB de la poutre. Si la déformation est importante, il faut tenir compte de la nouvelle position de l'extrémité B pour le calcul du moment en A.

Il n'y a pas de gauchissement des sections droites : Toute section plane et perpendiculaire à la ligne moyenne avant déformation reste plane et perpendiculaire à la ligne moyenne après déformation.

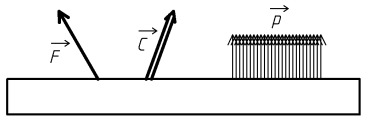
Une poutre peut être soumise à trois sortes d'actions extérieures :
Dans les zones éloignées des points d'applications des charges, la répartition des contraintes dans une section droite est indépendante des modes d'application.

Une section droite de poutre est une section plane perpendiculaire à la ligne moyenne de cette poutre. Elle sépare la poutre en deux parties, le tronçon de droite et le tronçon de gauche. Puisqu'elle coupe fictivement la poutre en deux parties, on la nomme section de coupure.
Dans une section droite, considérons une surface élémentaire (très petite) dS.
Sur cette surface, le tronçon de droite exerce sur tronçon de gauche
la force élémentaire

Le vecteur contrainte
Le vecteur contrainte

De manière générale, toute surface élémentaire à l'intérieur d'une pièce peut être soumis à une contrainte normale et à une contrainte tangentielle.
Une section de coupure étant choisie, isolons un des deux tronçons, par exemple celui de gauche. Ce tronçon de gauche est soumis :
Le tronçon de gauche est en équilibre. D'après le PFS :
{ T coh. } + { T ext. } = { 0 }
Cette relation permet de déterminer le torseur des efforts de cohésion au barycentre G de la section de coupure.
{ T coh. } =
G {

La résultante
De même, le moment

En tout point de la section de coupure :
En déplaçant la section de coupure tout le long de la poutre, on obtient les diverses valeurs des efforts normal et tranchant, des moments de flexion et de torsion. On peut alors tracer les diagrammes correspondants.

Cet essai est l'un des plus important en RDM.
Il consiste à exercer sur une éprouvette une force de traction

F : Force de traction exercée sur l'éprouvette, en N.
Lo : Longueur entre deux repères réalisés sur l'éprouvette au repos, en mm.
L : Longueur entre les deux repères sur l'éprouvette chargée, en mm.
Lu : Longueur ultime entre les deux repères sur l'éprouvette rompue, en mm.
So : Section de l'éprouvette au repos, en mm2.
S : Section de l'éprouvette chargée, en mm2.
Su : Section ultime de l'éprouvette rompue, en mm2.
Remarque : Le plan de rupture est souvent incliné de 45° environ.
Les courbes obtenues à partir de l'essai de traction comportent généralement deux zones.
Deux courbes de même forme sont tracées :

ΔL = L - Lo : Allongement, en mm.
ε =
σ =
Remarques :

E =
Re =
Rm =
A% =
Remarques :
Les moments quadratiques d'une section droite sont recherchés par rapport à un axe passant par le barycentre G de la section. Il est donc nécessaire de connaître la position de ce point.

Une surface se décompose en n surfaces dont on connaît les barycentres Gi et les aires Si. Soit O un point quelconque. La position du barycentre G de la surface se calcule avec la relation :
S1+S2+...+Sn représente l'aire totale de la surface. Pour des raisons pratiques, le point O est généralement l'origine du repère dans lequel s'écrivent les coordonnées des points Gi.
Pour une section droite d'aire S et de barycentre G :
IGz =
IGy =
| Section droite | IGz | IGy | ||
|---|---|---|---|---|
 |
||||
 |
IOy = IGy + S . d2

Pour une section droite d'aire S et de barycentre G :
IGx = IGy + IGz
| Section droite | IGx | |
|---|---|---|
 |
||
 |