La statique est la partie de la mécanique où l'on étudie l'équilibre des solides et les actions mécaniques qui leur sont appliquées.
"Donnez-moi un point d'appui et je soulèverai le monde", disait Archimède. La statique permet, dans cet exemple, de connaître la force obtenue pour soulever la charge en fonction de celle exercée à l'extrémité du levier. Le calcul des actions mécaniques est utile pour choisir ou dimensionner de nombreux éléments, comme un moteur électrique, un roulement à billes ou la section d’une poutre.
Si un corps 1 exerce une action mécanique sur un corps 2, alors le corps 2 exerce une action mécanique sur le corps 1 directement opposée.
Le principe des actions mutuelles se nomme aussi principe des actions réciproques.
Dans l'exemple ci-dessous, deux solides 1 et 2 sont en contact ponctuel. La force exercée par le solide 1 sur le solide 2 est directement opposée à celle exercée par le solide 2 sur le solide 1. Les deux forces ont même support, même norme mais sont de sens opposés.
Le principe des actions réciproques appliqué à deux forces qui s'opposent correspond à la troisième loi de Newton.
Isoler un système consiste à séparer l'univers en deux parties :
Les parois du système isolé constituent la frontière d'isolement entre le système isolé et son environnement.
Le système isolé :
Elle est exercée par un élément de l'environnement sur un élément du système isolé. Il ne faut pas la confondre avec une action mécanique intérieure, exercée par un élément du système isolé sur un autre élément du système isolé.
On distingue deux sortes d'action mécanique extérieure :
Soit une biellette, de centre de masse G, de poids négligeable, soumise à deux forces quelconques
Maintenant, si les deux forces
Un système isolé est en équilibre si, par rapport à un référentiel galiléen :
On peut considérer qu'un système en mouvement est en équilibre si :
Dans un référentiel galiléen, le principe d'inertie est vérifié : Le centre de masse d’un solide isolé ou pseudo-isolé est soit au repos, soit animé d’un mouvement rectiligne uniforme.
Dans cette définition :
Pour tout système isolé S en équilibre, on a :
La relation
Sous forme vectorielle, on obtient deux théorèmes.
Si le système isolé est soumis à des forces uniquement, on écrit :
On peut choisir n'importe quel point de calcul. Souvent, le problème est plus facile à résoudre si on prend comme point de calcul le point de réduction du torseur avec le plus d'inconnues.
Si le système isolé, en équilibre, est soumis à deux forces, alors ces deux forces sont directement opposées.
Si le système isolé, en équilibre, est soumis à trois forces non parallèles, alors :
La construction graphique de cette somme vectorielle se nomme triangle des forces, dynamique fermé ou encore polygone dynamique.
* C'est la conséquence du théorème du moment statique.
** C'est la conséquence du théorème de la résultante statique.
Elles sont géométriquement parfaites avec ou sans prise en compte du frottement. Lorsque le frottement est pris en compte, il est généralement modélisé avec la loi de Coulomb.
Les actions mécaniques engendrent sur les pièces des déformations, modifiant la géométrie du problème. Généralement, ces faibles déplacements influencent les résultats de manière insignifiante. On dit alors que les pièces sont considérées indéformables.
Si les actions mécaniques sont constituées de forces situées dans un même plan, de couples perpendiculaires à ce plan, on dit que le problème est plan.
Lorsque la disposition des actions mécaniques présente un plan de symétrie, le problème peut être ramené dans ce plan.
Certaines actions mécaniques, trop faibles pour influencer les résultats de manière significative, sont négligées. Par exemple, si le poids du système isolé est faible devant les autres actions mécaniques, alors il n'est pas pris en compte.
Un système est isostatique s’il est possible de déterminer les efforts auxquels il est soumis, en appliquant seulement le PFS.
Il est hyperstatique si, pour déterminer les efforts auxquels il est soumis, il est nécessaire, en plus des équations obtenues par le PFS, d’écrire des équations liées aux déformations de ce système. Ces déformations sont étudiées en résistance des matériaux.
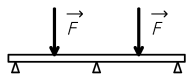
La poutre posée sur trois appuis est un exemple de problème hyperstatique.
Parfois, pour résoudre un problème de statique, il est nécessaire d’appliquer le PFS sur différents systèmes. Ces derniers sont isolés dans un ordre permettant la résolution progressive du problème.
Dans le cas d'une résolution analytique, soient Ni et Ne les nombres d’inconnues et d’équations indépendantes, obtenues en appliquant le PFS sur le système isolé.
Avant l'arrivée des ordinateurs, les méthodes graphiques étaient très utilisées. La tour Eiffel, par exemple, a été dimensionnée graphiquement. Les nombreuses méthodes graphiques portent différents noms.
De nos jours, la résolution graphique garde un intérêt pédagogique. En somme, si le système isolé est soumis à deux forces ou à trois forces concourantes, les deux méthodes de résolution sont possibles. Dans les autres cas, la résolution analytique s’impose.
Elle se présente en six étapes :
Remarque : Parfois, le problème se résout en appliquant le théorème de la résultante statique seulement. La quatrième étape est alors inutile.
Elle se présente en quatre étapes :
| Force | Point d'application | Direction/sens | Norme |
|---|---|---|---|
Remarque : Le BAME est communément présenté avec un tableau.