- IGz = ∫ y2 . dS
- IGy = ∫ z2 . dS
- IGx = IGy + IGz
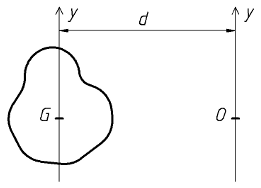
- IOy = IGy + S . d2
En résistance des matériaux, les moments quadratiques s'utilisent :
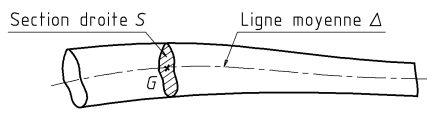
Une poutre est un solide de forme allongée. Pour être plus précis, c'est un solide engendré par le déplacement d'une surface plane S, dont le barycentre (ou centre de surface) G décrit une ligne Δ, perpendiculaire en tout point au plan contenant S. La ligne Δ est appelée "ligne moyenne".
Une section droite de poutre est une section plane perpendiculaire à la ligne moyenne de cette poutre.
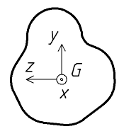
Ce sont des grandeurs caractéristiques de la géométrie d'une section droite. Elles se définissent par rapport à un axe.
Considérons une section droite de surface S et de barycentre G :
Les moments quadratiques se déterminent avec les relations ci-dessous.

La résolution des intégrales, ainsi que l'utilisation du théorème de Huygens, permettent d'obtenir les formules ci-dessous. Les sections choisies sont celles utilisées couramment en construction mécanique.
| Type de section | Moments quadratiques |
|---|---|
Tube rond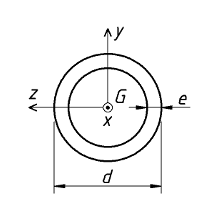 |
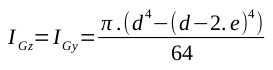 |
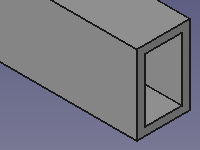
Tube rectangulaire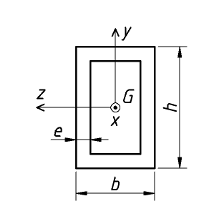 |
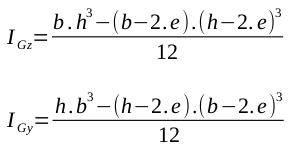 |
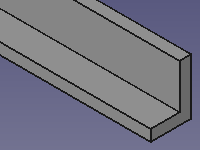
Cornière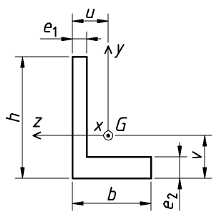 |
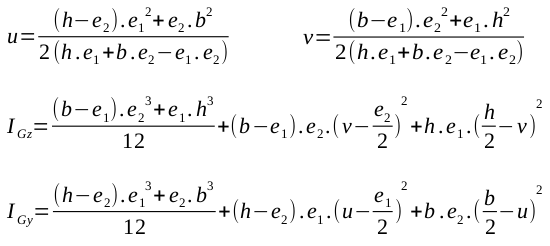 |
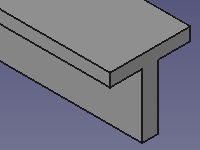
Poutre en T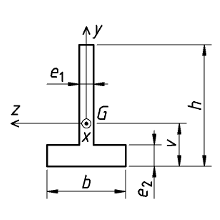 |
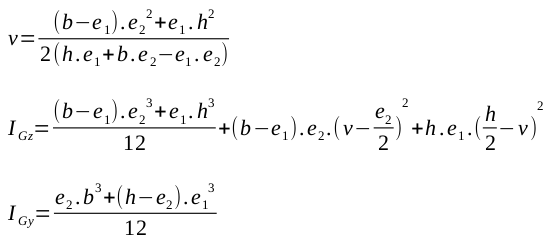 |
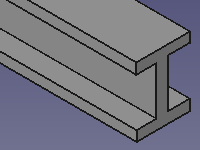
Poutre en H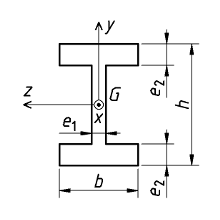 |
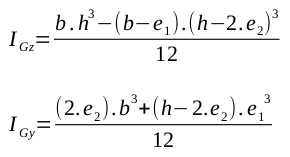 |
Poutre en U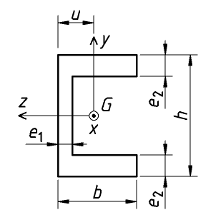 |
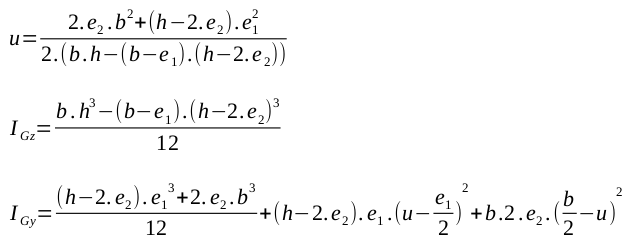 |
Afin de faciliter le travail des ingénieurs mécaniciens, on souhaite développer une application web. Elle permettra de calculer aisément les moments quadratiques des six sections de poutre présentées dans le formulaire ci-dessus.
Ci-dessous, on propose des vues en perspective de ces poutres. Elles ont été obtenues à l'aide d'un modeleur volumique.
 |
 |
 |
 |
 |
 |
L'utilisateur de l'application Web :
Conditions de travail :
Critères d'évaluation :