PYTHON
TRACER DES GRAPHIQUES

Objectif

Il s'agit ici de tracer des graphiques à l'aide de deux bibliothèques :

Matplotlib : Performante et populaire, elle permet de tracer des graphiques, de visualiser les données sous de nombreuses formes.
NumPy : Dédiée aux mathématiques, adaptée aux recherches de valeurs, elle manipule efficacement les matrices (tableaux multidimensionnels).

Les lignes de code seront écrites avec l'EDI (Environnement de Développement Intégré) EduPython.

Comprendre

Coordonnées connues

L'exemple basique ci-dessous utilise le module Pyplot de la bibliothèque Matplotlib.

# Importation de la bibliothèque
import matplotlib.pyplot as plt

# Coordonnées des points
liste_x = [1, 2, 4, 5, 7, 8]
liste_y = [1, 6, 9, 15, 12, 2]

# Affichage de la figure
plt.plot(liste_x, liste_y)
plt.show()

Cet exemple se complète avec le titre, la grille, la couleur...

import matplotlib.pyplot as plt

liste_x = [1, 2, 4, 5, 7, 8]
liste_y = [1, 6, 9, 15, 12, 2]

plt.title("Exemple de graphique")  # plt.figure("Exemple de graphique")
plt.xlabel("L'axe horizontal")
plt.ylabel("L'axe vertical")
plt.grid()

plt.plot(liste_x, liste_y, marker='o', color='#00ff00')
plt.show()

Autres tests

Tracer le graphique en rouge au lieu du vert.
Essayer d'autres valeurs pour le paramètre marker : 'x', '+', '*', 'H', 's'.
Changer la taille du marqueur : markersize='25'
Remplacer plt.plot(...) par :
- plt.bar(liste_x, liste_y) pour obtenir un histogramme.
- plt.scatter(liste_x, liste_y) pour produire un nuage de points.
- plt.pie(liste_x, labels = liste_y) pour créer un camembert.
Ecrire du texte à l'emplacement choisi : plt.text(2, 11, 'Courbe en cloche')
Modifier le titre, les qualificatifs pour les axes.
Retirer la grille.

Coordonnées calculées par Python

Ci-dessous, des listes sont initialisées puis complétées au fur et à mesure. Les coordonnées des points sont calculées par Python.

import matplotlib.pyplot as plt

liste_x=[]
for i in range(21) :
  x=-5+0.5*i
  liste_x.append(x)

liste_y=[]
for x in liste_x :
  y=x**2        # y=x**3   y=2*x-3
  liste_y.append(y)

plt.plot(liste_x, liste_y, marker='o')
plt.show()

Tester les fonctions placées en commentaire.

Variante

L'utilisation de listes en compréhension donne le même résultat avec une syntaxe bien plus courte.

import matplotlib.pyplot as plt

liste_x=[-5+0.5*i for i in range(21)]
liste_y=[x**2 for x in liste_x]

plt.plot(liste_x, liste_y, marker='o')
plt.show()

Autre variante

Le même résultat s'obtient avec une seule répétition se passant de la variable i :

import matplotlib.pyplot as plt

liste_x=[]
liste_y=[]
x=-5
while x<=5 :
  liste_x.append(x)
  y=x**2        # y=x**3   y=2*x-3
  liste_y.append(y)
  x+=0.5

plt.plot(liste_x, liste_y, marker='o')
plt.show()

Coordonnées calculées par NumPy

Matplotlib fonctionne avec les listes mais aussi avec les tableaux à une dimension (ou vecteurs) de NumPy. Les calculs s'effectuent bien plus rapidement. Les abscisses s'obtiennent alors avec les méthodes linspace() ou arange() de NumPy.

import matplotlib.pyplot as plt
import numpy as np

tab_x=np.linspace(-5,5,21)  # tab_x=np.arange(-5,5.5,0.5)
tab_y=tab_x**2              # tab_y=tab_x**3    tab_y=np.sin(tab_x)    tab_y=(25-tab_x**2)**0.5

plt.plot(tab_x, tab_y, marker='o')
plt.show()

Tester les fonctions placées en commentaire.

Pratiquer

Polygone

Obtenir le résultat ci-dessous :

Evolution du trafic

Cisco Systems, fabricant de routeurs et autres matériels pour réseaux, propose ce tableau montrant l'évolution du trafic mensuel sur Internet :

Année	2017	2018	2019	2020	2021	2022
Volume (Eo)	122	156	201	254	319	396

Ces valeurs se retrouvent avec la formule :

Volume = 5 × (Année - 2014)² + 76

Tracer l'histogramme montrant l'évolution du trafic sur Internet :

A partir de la formule.
En calculant les coordonnées par Python (sans utiliser NumPy).

Raréfaction des adresses IPv4

L'évolution annuelle du nombre d'adresses IPv4 disponibles au RIPE-NCC, en millions, est donnée par la formule :

Nombre = 10 × [rac]2020,25 - Année[/rac] - 5

A l'aide de NumPy, tracer la courbe montrant l'évolution du nombre d'adresses IPv4 disponibles, pour les années allant de 2015 à 2020.

Approfondir

Diagramme de Gantt

De manière très simplifiée, la construction d'une maison passe par les étapes :

Le coulage des fondations sur la journée, avec un durcissement du béton de 5 jours.
Le montage des murs, s'effectuant en 3 jours.
La pose du toit, nécessitant 4 jours.

Un diagramme de Gantt visualise ces tâches.

import matplotlib.pyplot as plt

travaux = ["Fondations", "Murs", "Toit"]
debut = [0, 5, 8]
fin = [1, 8, 12]

# Inversion des listes, facultatif
travaux = list(reversed(travaux))
debut = list(reversed(debut))
fin = list(reversed(fin))

# Histogrammes horizontaux
plt.barh(travaux, fin, color='#669900')
plt.barh(travaux, debut, color='#ffffff')

# Ajout de titres pour l'axe vertical et la figure
plt.xlabel("Jours")
plt.title("Planification des travaux")

# Affichage du diagramme de Gantt
plt.show()

Compléter ce diagramme de Gantt sachant que les menuiseries extérieures :

Se posent en 2 jours.
En même temps que le toit.

Deux courbes sur un même graphique

Tracer, sur un même graphique, les courbes de y₁ et y₂ en fonction de x.

x varie de 0 à 2π
y₁ = sin x + 1
y₂ = [rac]x[/rac]

Graphique en 3D

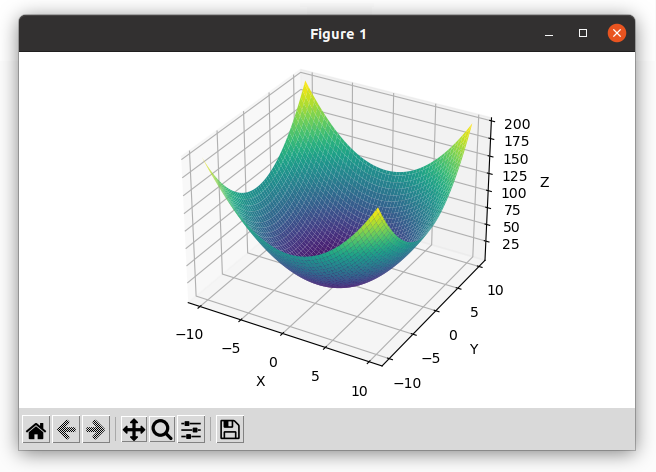
Tester le programme ci-dessous puis l'adapter à d'autres équations, par exemple :

z = [rac]x² + y²[/rac]
z = x² - y²
z = x³ - y³
z = sin x + cos y
z = sin[par][rac]x² + y²[/rac]
z = x . 2^{-(x² + y²)}

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Valeurs pour x, y et z
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
x, y = np.meshgrid(x, y)
z = x**2 + y**2

# Création de la figure 3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')

# Ajout de qualificatifs aux axes
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

# Affichage du graphique
plt.show()