TRIANGULATION
PAR RELEVE DE DISTANCES
Mise en situation
Un promeneur se perd dans la forêt landaise.
Equipé d'une carte, d'une boussole, d'une montre, il cherche sa position sur la carte.
Il entend sonner les horloges de trois églises environnantes, facilement identifiables.
Hypothèses et données
- Précisions des horloges, de la montre : Excellente
- Vitesse du son dans l'air : c = 340 m/s
- Instant auquel les horloges des églises sonnent : 15h précises
- Au regard de sa montre, le promeneur entend les horloges sonner à trois instants distincts :
| Eglise | Instant mesuré |
|---|
| Saint-Julien-en-Born | 15h 0min 5s |
| Uza | 15h 0min 6,5s |
| Lit-et-Mixe | 15h 0min 10s |
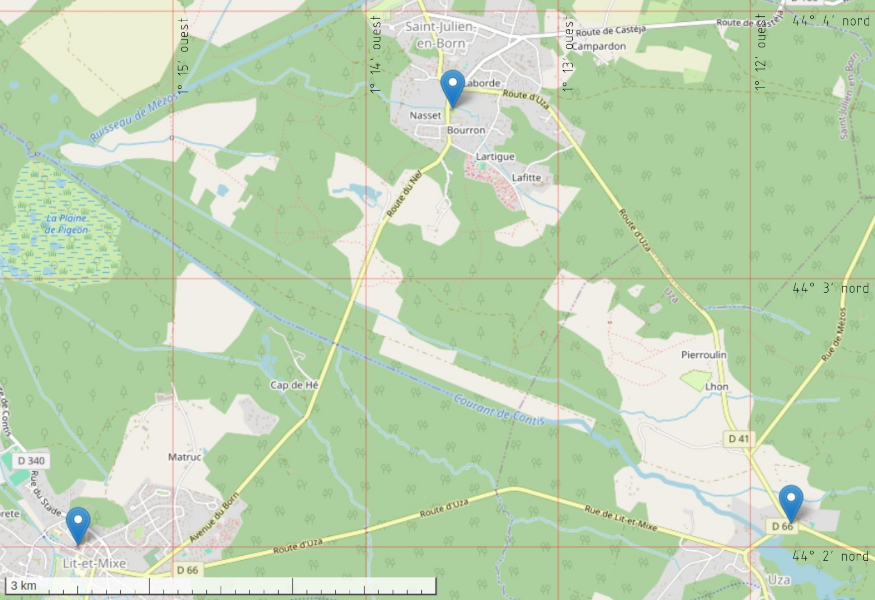
- Coordonnées géographiques :
| Eglise | Latitude | Longitude |
|---|
| Saint-Julien-en-Born | 44° 3' 38" nord | 1° 13' 33" ouest |
| Uza | 44° 2' 5" nord | 1° 11' 48" ouest |
| Lit-et-Mixe | 44° 2' 0" nord | 1° 15' 30" ouest |
Etude demandée
- La carte comporte une échelle graphique. Retrouver l'échelle numérique (forme 1 : ...).
- Calculer les distances d1, d2 et d3,
en km, entre le promeneur et les trois églises.
- Tracer la position du promeneur sur la carte.
- Quelles sont ses coordonnées géographiques, dans les systèmes sexagésimal et décimal?
- Quelle distance d, en km, sépare le promeneur de la route la plus proche?
- Vers quelle direction doit-il se diriger pour regagner cette route au plus vite?
- Si la montre du promeneur manquait de précision,
pourrait-il tout de même trouver sa position?