RELATIONS D'AMITIE
Mise en situation
Le but est de représenter sous forme mathématique un réseau social,
d'en définir les caractéristiques principales.
Hypothèses et données
- Le réseau social compte 8 membres : Ana, Brice, Cloé, Daniel, Eva, Fanie, Gaël et Hugo.
- Les membres se repèrent a, b, c, d, e, f, g et h.
- L'ensemble des membres se note E = { a, b, c, d, e, f, g, h }
- Une relation d'amitié se note avec un ensemble, par exemple {a,b} signifie "a et b sont amis".
- L'ensemble des relations d'amitié se note : RA = { {a,b}, {c,d}, ... }
- Une étude fournit les relations d'amitié réciproque pour chaque membre :
| Membre | Amis |
|---|
| Ana | Cloé, Fanie, Gaël |
| Brice | Eva, Hugo |
| Cloé | Ana, Daniel, Fanie |
| Daniel | Cloé, Eva |
| Eva | Brice, Daniel, Fanie |
| Fanie | Ana, Cloé, Eva |
| Gaël | Ana |
| Hugo | Brice |
Etude demandée
- Montrer les relations d'amitié en parachevant la représentation graphique.
- Définir l'ensemble RA (sans doublon).
- Compléter le tableau indiquant les distances entre les membres.
- Déterminer l'excentricité de chaque sommet.
- En déduire, pour ce graphe, le(s) centre(s), le rayon et le diamètre.
Représentation graphique
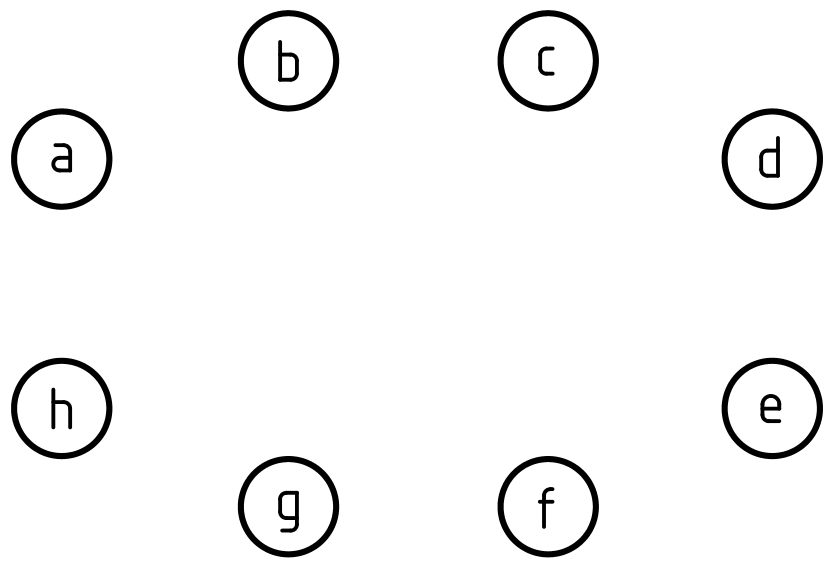
Ensemble des relations d'amitié
RA = {
Distances entre les membres
| Distance |
a |
b |
c |
d |
e |
f |
g |
h |
| a | X | | | | | | | |
|---|
| b | | X | | | | | | |
|---|
| c | | | X | | | | | |
|---|
| d | | | | X | | | | |
|---|
| e | | | | | X | | | |
|---|
| f | | | | | | X | | |
|---|
| g | | | | | | | X | |
|---|
| h | | | | | | | | X |
|---|
Excentricité des sommets
| Sommet |
a |
b |
c |
d |
e |
f |
g |
h |
| Excentricité |
| | | | | | | |
|---|
Caractéristiques du graphe
