MOTO-REDUCTEUR

Calculs de l'engrenage, des roulements

Mise en situation

L'objectif de l'étude est double :

• Choisir le matériau adéquat pour usiner les roues dentées du moto-réducteur.
• Déterminer les durées de vie des roulements pour mettre en place une procédure de maintenance.

Hypothèses et données

• Vitesse de rotation de l’arbre 2 : N₂ = 1470 tr/min
• Force transmise au niveau de l'engrènement : F = 1000 N
• Angle de pression (engrenage normalisé) : α = 20°
• Charge radiale supportée par le roulement 10 : F₁₀ = 500 N
• Charge radiale supportée par le roulement 11 : F₁₁ = 1500 N
• Charges axiales supportées par les roulements : Nulle
• Extrait de catalogue :

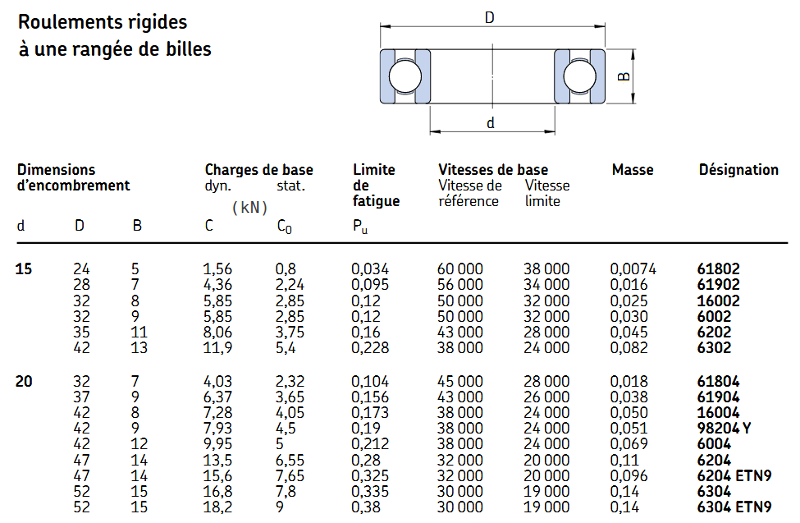
Etude demandée

Rapport de transmission

Questions générales pour une roue à denture droite :

1. Dans quelle unité s'exprime le module m?
2. Quelle relation y a-t-il entre le pas p et le module m?
3. Quelle relation y a-t-il entre le pas p, le nombre de dents Z et le périmètre c du cylindre primitif?
4. Le diamètre du cylindre primitif étant noté d, démontrer la relation d = m . Z
5. Quelle est la forme du profil d'une dent de roue dentée?

Questions relatives au moto-réducteur :

1. L'engrenage de ce moto-réducteur est-il parallèle, concourant ou gauche?
2. D'après la nomenclature, quelle est la valeur du module m de l'engrenage?
3. Mesurer, sur le dessin d'ensemble, les diamètres primitifs d₆ et d₁₅. En déduire les nombres de dents Z₆ et Z₁₅.
4. Calculer l'entraxe (la distance qui sépare les axes des deux roues dentées).
5. Déterminer le rapport de transmission r de l'engrenage.
6. En déduire la vitesse de rotation N₉, en tr/min, de l'arbre de sortie 9.

Calcul de l'engrenage

Déterminer l'acier le plus approprié pour fabriquer les roues dentées de ce moto-réducteur.

• Matériaux disponibles : Aciers S 235, S 275 ou S 355, de résistances limites élastiques respectives 235, 275 et 355 Mpa.
• Coefficient de sécurité souhaité : 2
• Formules de calculs :    m = 2,34 . Ftk . Rpe       Ft = F . cos(α)       k = bm       Rpe = Res
  m : Module, en mm (indiqué dans la nomenclature).
  Ft : Force tangentielle, en N.
  k : Coefficient de largeur de denture.
  Rpe : Résistance pratique à l'extension du matériau, en Mpa ou N/mm².
  F : Force transmise au niveau de l'engrènement, en N.
  α : Angle de pression.
  b : Largeur de denture, en mm (à mesurer sur le dessin d'ensemble).
  Re : Résistance élastique du matériau, en Mpa.
  s : Coefficient de sécurité.

Durée de vie des roulements

Questions préliminaires :

1. Quel est le type d'ajustement :
   • Sur les bagues extérieures des roulements?
   • Sur les bagues intérieures?
2. L'arrêt axial de l'arbre 9 se fait-il sur un roulement ou sur deux roulements?

Déterminer les durées de vie en heures des roulements 10 et 11, à l'aide de l'extrait de catalogue.

• Règles de montage des roulements :
  • La bague tournante d'un roulement, par rapport à la direction de la charge, est montée avec un ajustement serré sur sa portée.
  • La bague fixe d'un roulement, par rapport à la direction de la charge, est montée avec un ajustement glissant sur sa portée.
• Un roulement à billes peut supporter une charge axiale Fa et une charge radiale Fr. La charge radiale équivalente P se calcule en fonction de Fa et Fr, selon la documentation fournie par le fabriquant. Si Fa = 0 alors P = Fr.
• La durée de vie d'un roulement à billes se calcule avec les relations :
  
  
  • L₁₀ = CP3     en millions de tours
  • L₁₀ = CP3 . 10⁶60 . N    en heures