PINCE DE BRAS MANIPULATEUR

Etude statique

Mise en situation

Le but de cette étude est de connaître les forces exercées par les phalanges 4 sur la pièce à manipuler, en fonction :

• De leurs positions.
• De la pression d'alimentation en air comprimé.

Hypothèses et données

• Pression d'alimentation : 6 bars.
• Sont négligés :
  • Les poids des pièces.
  • Les frottements.
  • Les forces exercées par les ressorts.
• Lorsque la pince est fermée, les phalanges sont horizontales (et non inclinée, comme dans le cas de la pince ouverte).
• Les forces exercées par les phalanges sur la pièce ont pour support la droite verticale passant l'extrémité des phalanges.

Etude demandée

Etape 1

Il s'agit ici de se rendre compte des positions prises par les diverses pièces, lorsque la pince se ferme. Pour cela, esquisser les formes générales de la pince (contours des pièces 2, 4 et 5), en position fermée. En déduire :

• L'inclinaison des biellettes 5, par rapport à la verticale, pour la pince fermée.
• La course du piston 2.

Etape 2

Calculer la résultante des forces de pression exercées par l'air comprimé sur le piston 2.

Etape 3

Isoler l'ensemble des pièces S = { 2, 7, 13 }. Prendre en compte les actions mécaniques extérieures suivantes :

• L'action de l'air comprimé sur le piston 2, de résultante la force G, de point d'application E.
• Les actions des biellettes 5, assimilées à deux forces A₁ (biellette supérieure) et A₂ (biellette inférieure). On suppose que ces forces :
  • Ont pour point d'application le point B, situé au centre de l'axe de piston 7.
  • Ont pour directions celles des biellettes.
  • Sont situées dans le plan de symétrie de la pince.
  • Ont même norme vue la symétrie du système.

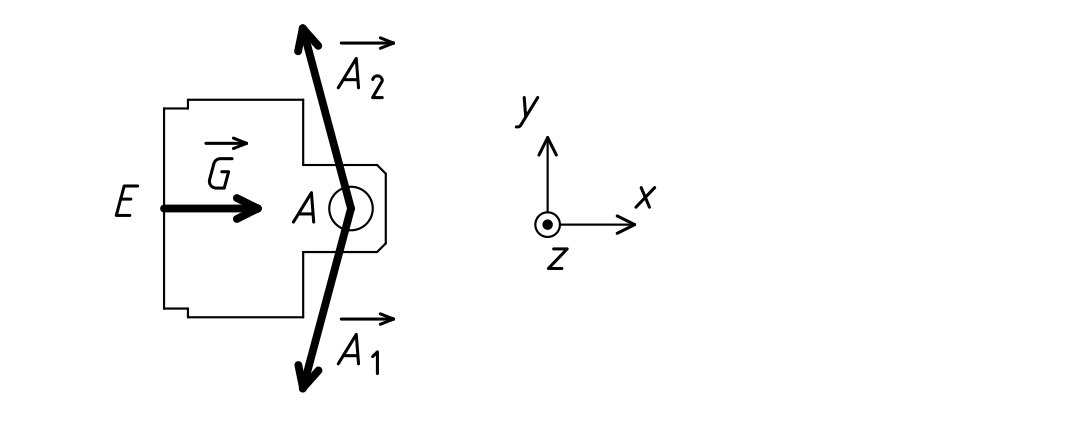
Appliquer le théorème de la résultante statique pour déterminer les normes de A₁ et A₂.

Etape 4

Isoler la phalange supérieure 4. Prendre en compte les actions mécaniques extérieures suivantes :

• L'action de la pièce à manipuler sur la phalange, force H dirigée vers le haut et de point d'application son extrémité F.
• L'action de la biellette 5, force B₁ de point d'application B, telle que B₁ = - A₁
• L'action de l'axe 6, force R de point d'application D.

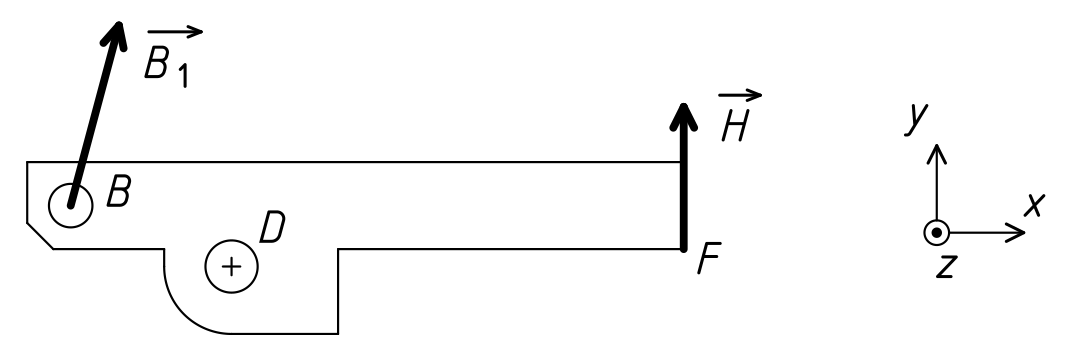
Appliquer le théorème du moment statique pour déterminer la norme de H.

Pour les audacieux

On propose le schéma suivant :

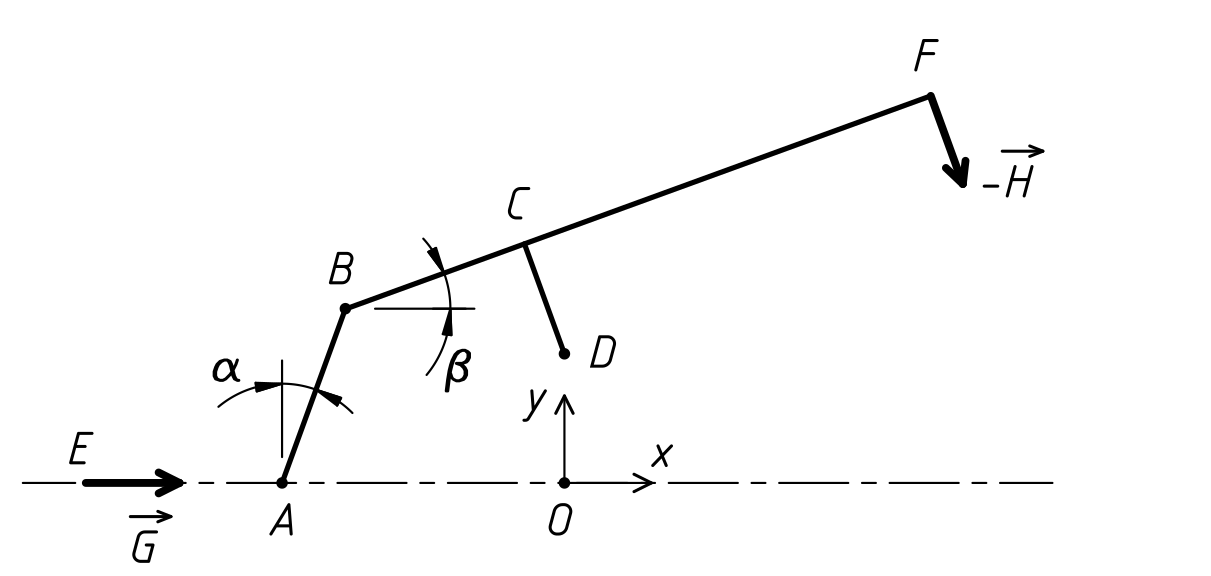
Compléter le programme en Python ci-dessous pour tracer la courbe donnant la norme de la force -H en N exercée sur la pièce à saisir en fonction de la position du piston x_A en mm.

import matplotlib.pyplot as plt
import numpy as np

# Dimensions mesurées sur le dessin d'ensemble (échelle 2:1)
AB = 31/2
BC = 37/2
DC = 14/2
OD = 16/2

# Valeurs choisies pour l'inclinaison de la phalange 4 par rapport à l'horizontale 
beta_deg = np.linspace(-1,13,5000)
beta_rad = beta_deg*np.pi/180 

# Calculs des coordonnées des points
xD = 0
yD = OD
xC = -DC*np.sin(beta_rad)
yC = OD+DC*np.cos(beta_rad)
xB = -DC*np.sin(beta_rad)-BC*np.cos(beta_rad)
yB = OD+DC*np.cos(beta_rad)-BC*np.sin(beta_rad)
xA = xB-(AB**2-yB**2)**0.5
yA = 0

# Calcul de l'inclinaison de la bielette 5 par rapport à la verticale
alpha_rad = np.arctan((xB-xA)/yB)
alpha_deg = alpha_rad*180/np.pi

# Tracé d'une courbe
plt.xlabel("xA (mm)")
plt.ylabel("Beta (°)")
plt.grid()
plt.plot(xA, beta_deg)
plt.show() 

Courbe obtenue :