PYTHON
METHODES NUMERIQUES
EXEMPLE PRATIQUE - 2EME PARTIE

Mise en situation

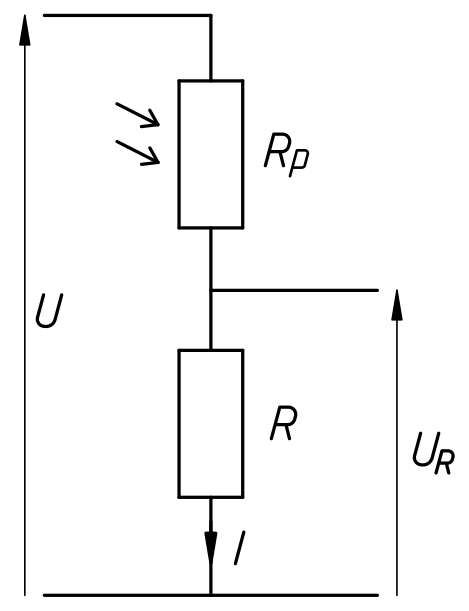
Une photorésistance se place habituellement en série avec une résistance de 10 kΩ, de sorte que la lumière reçue par la photorésistance s'évalue en mesurant la tension aux bornes d'un des deux composants. L'étude précédente montrait que pour une luminosité variant nettement, ces 10 kΩ pouvait avantageusement se remplacer par une valeur plus petite, comme 4 kΩ par exemple.

Qu'en est-il pour une plage de luminosité plus réduite? Les deux méthodes, numérique et analytique, seront mises en œuvre.

Hypothèses et données

Notations

• U : Tension d'alimentation, en V
• I : Courant dans le circuit, en A
• R_P : Valeur de la photorésistance, en Ω
• R : Valeur de la résistance, en Ω
• U_R : Tension aux bornes de la résistance, en V
• R_P max, R_P min : Valeurs de la photorésistance peu à fortement éclairée, en Ω
• ΔU = U_R max - U_R min : Plage de tension aux bornes de la résistance, en V

Schéma électronique

Valeurs retenues

• U = 5 V
• R_P min varie de 70 Ω à 700 Ω
• R_P max varie 10 kΩ à 100 kΩ

Etude demandée

• Les valeurs extrêmes de R_P dépendent de la luminosité et du modèle de photorésistance. Tracer la courbe donnant les valeurs de R optimales selon diverses valeurs extrêmes de R_P. Faire varier :
  • R_P min de 70 Ω à 700 Ω
  • R_P max de 10 kΩ à 100 kΩ
• Conclure.

Compte rendu

Programmes en python

Solution numérique

#!/usr/bin/python3

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Valeurs pour Rpm et RpM, en Ω
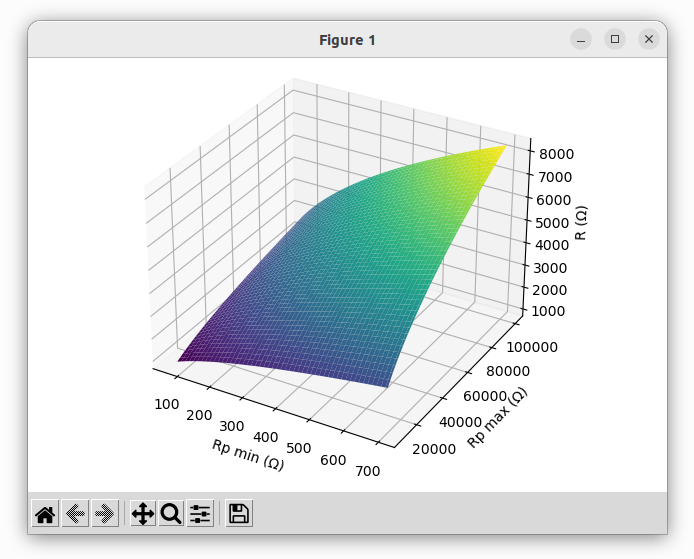
Rpm = np.linspace(70, 700, 100)
RpM = np.linspace(10000, 100000, 100)
Rpm, RpM = np.meshgrid(Rpm, RpM)

# Fonction pour calculer la résistance optimale
def calcul_R_op(Rpm, RpM):
    U = 5
    R = np.linspace(500, 20000, 500)
    delta_U = R*U*(1/(Rpm+R)-1/(RpM+R))
    liste_R = list(R)
    liste_delta_U = list(delta_U)
    R_rech = liste_R[liste_delta_U.index(max(liste_delta_U))]
    return round(R_rech)

# Résistance optimale, en Ω
R_op = np.vectorize(calcul_R_op)(Rpm, RpM)

# Tracé de la courbe
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(Rpm, RpM, R_op, cmap='viridis')
ax.set_xlabel('Rp min (Ω)')
ax.set_ylabel('Rp max (Ω)')
ax.set_zlabel('R (Ω)')
plt.show()

Solution analytique

#!/usr/bin/python3

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Valeurs pour Rpm et RpM, en Ω
Rpm = np.linspace(70, 700, 100)
RpM = np.linspace(10000, 100000, 100)
Rpm, RpM = np.meshgrid(Rpm, RpM)

# Résistance optimale, en Ω
R_op = (Rpm*RpM)**0.5

# Tracé de la courbe
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(Rpm, RpM, R_op, cmap='viridis')
ax.set_xlabel('Rp min (Ω)')
ax.set_ylabel('Rp max (Ω)')
ax.set_zlabel('R (Ω)')
plt.show()

Courbe obtenue

Conclusion

• Pour une faible luminosité variant peu, on a intérêt à prendre une résistance assez importante, 10 kΩ par exemple.
• Pour une luminosité variant davantage, une résistance moins grande est mieux adaptée, même si la résistance de 10 kΩ convient.